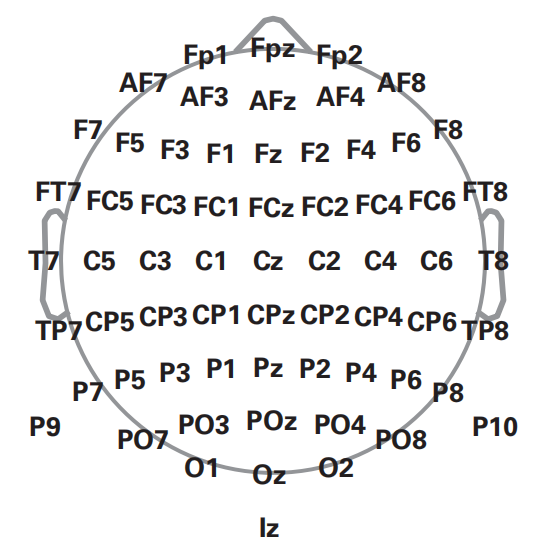
2-D topographical ocations of EEG electrodes

64 electrodes

Brain rhythm frequency bands

delta (2(0.5)-4 Hz)

theta (4-8 Hz)

alpha (8-12 Hz)

beta (15-30 Hz)

lower gamma (30-80 Hz)

upper gamma (80-150 Hz)

subdelta and omega (up to 600 Hz)

Intra- and Intertrial Timing

*Intratrial*：单个trail内。
*Intertial*: 不同trial之间。the duration of time between the end of one trial and the start of the next trial

Phase-Locked and Nonphase-Locked

7 | 数据预处理

The Balance between Signal and Noise | 信号与噪声的取舍平衡

保留更多的信号通常也意味着保留更多的噪声。

某些数据是信号还是噪声取决于实验的目的。

Creating Epochs

提取epoch的过程可以认为是将一段完整的数据划分成不同的小段

1. 如何选择“time=0”的时刻

对于大多数实验，选择刺激开始的时刻作为time=0
对于其他情况，如有多个刺激时，可选择第一个刺激或最关键的刺激开始的时刻作为time=0
time-lock（time=0时刻的选择）是可以根据需要调节变化的

2. time=0前后需要包含多长时间

对于ERPs分析，划分的小段只需要包含你想要分析的时间段加上baseline，例如相对于0时刻的-200ms到800ms。

对于时频分析，需要划分更长的时间段，以避免边缘伪影（edge artifacts），即需要预留足够长的缓冲区，使边缘伪影消退。此外，提取的频带越小，需要预留的缓冲区也应该越长。在时频功率谱中，边缘伪影很容易识别，因此可以先试分析一组数据再确定需要预留的缓冲区长度。通常情况下，将缓冲区长度设置为所分析的最低频率所对应的三个周期就足够了（例如，对2Hz的频率，设置缓冲区为1500ms）。

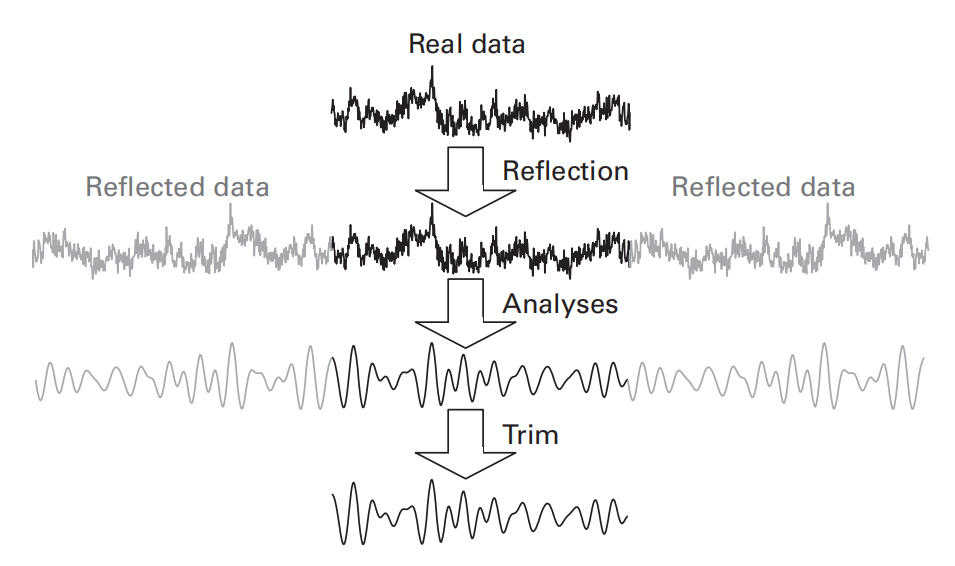
如果划分的epoch不够长，可以使用“reflection”的方法，即将这一段数据关于开始和结尾时刻首尾对称一下，再拼接到数据前和数据后，这样就可以得到三倍长的epoch。

Matching Trial Count across Conditions | Trial数量的设置与平衡

1. 不同的实验条件尽量设置相同的trial数：

理想情况下，所有条件（例如实验设计中的不同实验条件或组别）应该有相同数量的试验。这样可以确保分析结果的公平性和可比性。

2. trial数量对不同分析的影响：

基于相位的分析：相位分析对试验数量特别敏感。如果trial数量较少，结果中会出现正偏差（positive bias），即trial数量少的实验条件可能显示出更大的结果。这是因为相位分析对于小样本量更容易受到随机波动的影响，导致条件间结果的偏差。
基于功率的分析：功率分析也可能出现一些正偏差。因为功率值通常是正值，数据中的噪声更倾向于增加功率值，所以较少的试验数量可能导致功率结果偏高。

3. 应对低trial数量的方法：

对于ERP分析，如果试验数量较少，与其依赖峰值时间（peak times）的分析，不如取一段时间范围内的平均幅值（mean amplitude）。这种方法对噪声更为稳健，不容易受到个别异常值的影响。

4. 应对不同实验条件的trial数量不一致的方法：

如果出现不同的实验条件下的trial数目不一致，假设最小的trial数为N，那么可以通过以下方法来平衡trial数：

（不建议采用）直接选前N个trial
随机选N个trial
根据一些相关的行为或实验变量，如反应时间等，有目的地选N个trial

Trial Rejection

9 | Overview of Time-Domain EEG Analyses

To create ERPs, simply align the time-domain EEG to the time=0 event (this was probably already done during preprocessing) and average across trials at each time point.

指定 time points
trial average

Butterfly Plots

A butterfly ploy shows the ERP from all electrodes overlaid in the same figure.

Global Field Power / Topographical Variance Plots

The global field power is the standard deviation of activity over all electrodes.

The Flicker Effect

The flicker effect in EEG research refers to entrainment of brain activity to a rhythmic extrinsic driving factor. This effect is also referred to as steady-state evoked potential, frequency tagging, SSVEP (steady-state visual evoked potential), SSAEP (auditory evoked potential), or something similar.

The flicker effect is arguably an underutilized tool in cognitive electrophysiology. The main benefit of the flicker effect is that it allows you to “ tag ” the processing of a specific stimulus.

(from ChatGPT)

假设你正在进行一项视觉注意力的研究，目的是研究大脑如何同时处理多个视觉刺激。你在屏幕上呈现两个物体：一个物体以12 Hz的频率闪烁（即每秒闪烁12次），另一个物体以15 Hz的频率闪烁。你让参与者专注于两个物体之一，然后使用EEG记录他们的大脑活动。

在这种情况下，闪烁效应会导致大脑中处理视觉信息的区域（通常是视觉皮层）出现与这两个频率相对应的节律性活动。12 Hz的物体会在大脑中产生12 Hz的节律性活动，15 Hz的物体会产生15 Hz的节律性活动。通过分析EEG数据中的频率成分，你可以识别出大脑中对应这两个不同频率的活动区域。

即使EEG无法像功能性磁共振成像（fMRI）那样精确地显示大脑中具体的活动区域，你仍然可以通过这些频率标记来“分离”出大脑中对12 Hz和15 Hz刺激分别作出反应的神经元群体。换句话说，虽然EEG的空间分辨率较低，但通过闪烁效应，你可以“假设”出对不同刺激反应的特定神经区域。

具体的例子说明：

12 Hz闪烁的物体：如果参与者主要关注这个物体，你会看到EEG数据中12 Hz频率的功率增加，这表明视觉皮层中的某个区域在处理这个物体。
15 Hz闪烁的物体：如果参与者关注这个物体，EEG数据中15 Hz频率的功率会增加，显示另一个区域在处理这个物体。

通过这种方法，即使两个物体在大脑中产生的活动区域相距较近，由于频率不同，你依然能够区分开来。这就相当于“模拟”出了一种高空间分辨率，使得你可以推断大脑中不同区域对不同刺激的反应。

Topographical Maps

Creating a topographical map is conceptually similar to interpolating an electrode, except that instead of estimating the activity at one point in space corresponding to a missing electrode, activity is estimated at many point in space between electrodes.

topoplot()

Microstates

In EEG as well as ERP map series, for brief, subsecond time periods, map landscapes typically remain quasi-stable, then change very quickly into different landscapes.

Durations tend to be around the alpha range (70-130 ms), and topographical distributions tend to fit into four or five distinct patterns.

ERP Images

An ERP image is a 2-D representation of the EEG data from a single electrode. Rather than all trials averaged together to form an ERP, the single-trial EEG traces are stacked vertically and then color coded to show changes in amplitude as changes in color.

10&11 | 卷积、傅里叶变换

一段关于卷积、离散傅里叶变换（DFT）和快速傅里叶变换（FFT）的视频：

【官方双语】那么……什么是卷积？

Supplementary Code for Figure 11.5

对于书中所提供的图11.5对应代码的一些细节注释

%% Figure 11.5

N       = 10;         % length of sequence  长度为10的向量
data    = randn(1,N); % random numbers
srate   = 200;        % sampling rate in Hz 采样率200Hz
nyquist = srate/2;    % Nyquist frequency -- the highest frequency you can measure in the data


% initialize Fourier output matrix
fourier = zeros(size(data)); 

% These are the actual frequencies in Hz that will be returned by the
% Fourier transform. The number of unique frequencies we can measure is
% exactly 1/2 of the number of data points in the time series (plus DC). 
% 一个长度为 N 的信号需要 N 个正交基（frequency）才能完全表示
% 但在这里只保留了N/2+1个frequencies，是因为对于实数值信号，负频率与正频率对应的幅值、相位信息是对称的
% 所以舍去了N/2个负频率
frequencies = linspace(0,nyquist,N/2+1);   % 生成的频率从 0 到 100 Hz，共有 N/2 + 1 个点，间隔为srate/N
time = ((1:N)-1)/N;

% Fourier transform is dot-product between sine wave and data at each frequency
for fi=1:N      
    % fi（归一化频率，index，无单位）有N个取值，与frequencies（物理频率，Hz）为线性映射关系
    % 所以使用这两种频率DFT后的结果一致（幅值、相位相等）
    sine_wave   = exp(-1i*2*pi*(fi-1).*time);
    fourier(fi) = sum(sine_wave.*data);
end
fourier=fourier/N;  % 归一化，使得振幅具有实际意义，并保证能量的一致性

The Fast Fourier Transform | FFT

如何将 fft 函数的输出与实际的频率和幅值对应起来：

采样率：$F_s$ 采样点数：$N$
FFT后向量中某点索引：$n$
- 该点频率：$f_n=(n-1)\cdot F_s/N$
- 该点幅值：$abs(Result_{FFT})/(N/2)$

12 | 小波 Wavelet

How to Wake Wavelets | 小波的创造

不同于使用傅里叶变换进行的分析，使用小波变换时小波的频率和数目可以自行选择。一组具有相同性质但频率不同的小波叫作小波族，构造一组小波族有如下限制：

不能用比你划分的时间小段（epochs）更慢的频率。例如，你有一段1s长的数据，那么你不能分析低于1Hz的活动，应该让这1s中包含多个活动周期，建议使用4Hz或更快的小波。
小波的频率不能高于奈奎斯特频率（采样率的一半）
选择相近的频率所获得的结果会很相近（例如15.0Hz和14.9Hz），且越密集的频率所需要的计算时间会越长，一般而言，在3Hz到60Hz之间选择15到30个频率就够了。

13 | Complex Morlet Wavelets (cmw)

Create complex sine wave

复数域的Wavelet函数也是由sine函数和Gaussian相乘得来，只是所使用的sine函数是在复数域表示的（ $e^{i2\pi ft}$ ）

$cmw=Ae^{-t^2/2s^2}e^{i2\pi ft}$ (the x-axis offset for Gaussian are omitted)
$A=\frac{1}{(s\sqrt{\pi})^{1/2}}$

The Result of cmw

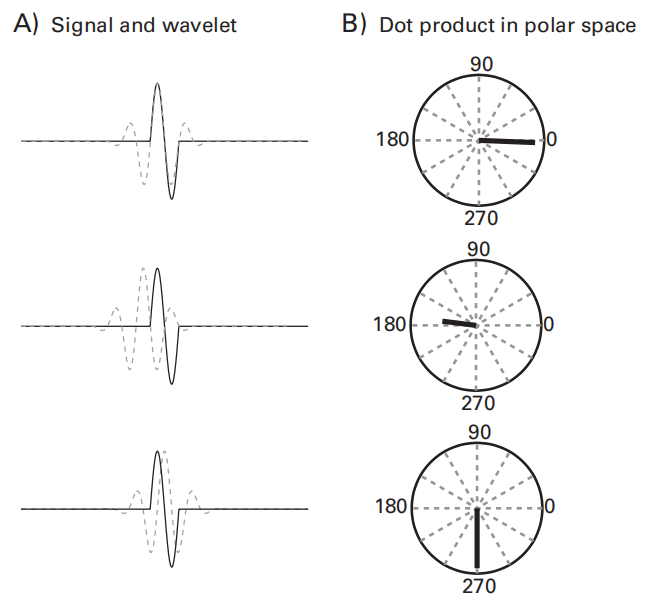
复数wavelet与信号点积的结果有三个维度：时间、实部、虚部。将该结果绘制在复平面上，其在实轴、虚轴上的投影分别对应于wavelet的实部、虚部与信号的点积结果。

点积结果在复平面上所对应向量的长度反映了信号（signal）和核（kernal）的相似（重叠）程度，而且该长度与二者间的相位关系无关。相位关系由向量与实轴的夹角表示。

在实轴上的投影：带通滤波信号，其正负符号反映相位关系
向量长度（振幅）：反映wavelet与signal的相似性或重叠度，其平方称为功率
- abs(X).^2; or X.*conj(X); (乘以共轭)
与实轴夹角：反映了在wavelet中心时间点（即分析时段的中间时刻）和wavelet的主频率（即小波的主要振荡频率）下，信号的相位信息。
- angle(X);
上述提到的功率和相位值只能作为估计值，因为它们会受到邻近时间点活动的影响。

Parameters of Wavelets

最低频率
- 如果关注alpha-band activity，大概在5或6Hz即可
- 划分的时间区段（epoch）尽可能包含多个周期（如果epoch长1s，则不要低于4Hz）
最高频率
- 不能超过奈奎斯特频率（采样率的一半）
- 单个wavelet周期尽可能包含更多的信号数据点，可以提高信噪比
- 没有特别的期望的话，可能选择4Hz到6Hz的频率范围
频率数目
- 一般取20-30个频率足够覆盖较宽的频率范围。条件允许的情况下当然是越多越好，但是相近的频率不一定能提供更多信息。

频率分布间隔

线性分布

突出频谱的高频段

可以直接使用 imagesc(EEG.times,frequencies,tf_data); 绘图

imagesc(EEG.times,frex,eegpower)
set(gca,'clim',[-3 3],'xlim',[-200 1000],'ydir','norm')
title('WRONG Y-AXIS LABELS!!!!')
ylabel('Frequency (Hz)'), xlabel('Time (ms)')

对数分布（推荐）：

4-8Hz（theta）和30-80Hz（lower gamma）在y轴上占据的宽度会比较接近
突出频谱的低频段

使用 imagesc(EEG.times,[],tf_data) 绘图

imagesc(EEG.times,[],eegpower)
set(gca,'clim',[-3 3],'xlim',[-200 1000],'ydir','norm')
set(gca,'ytick',1:6:num_frex,'yticklabel',round(logspace(log10(min_freq),log10(max_freq),6)*10)/10)		% important!
title('CORRECT Y-AXIS LABELS!!!!')
xlabel('Time (ms)')

wavelets 的长度
- 要足够长，使得两侧能衰减到0（接近0）
- 没有长度限制，如果 -1s ~ +1s 不够，就设置成 -2s ~ +2s，不同的频率长度也不一定要相同
- wavelet 的图像要设置在时间轴中央（关于中间时刻对称），最简单的方法是将时间范围设置成 -x seconds to +x seconds
- wavelet 的采样率要和 EEG.data 一致
Gaussian函数要包含多少个周期
- “包含的周期数目”指的是Gaussian函数标准差公式 $s=\frac{n}{2\pi f}$ 中的 $n$
- 包含周期数越多，频率精度越高，时间精度越低
- 包含周期的数目也可随频率改变
- 应至少包含3个周期，至多包含14个周期
- 在wavelet的非零段，需要保证数据（进行卷积的信号片段）的平稳性（均值、方差等统计特性保持稳定）

相邻频率对小波卷积的贡献程度

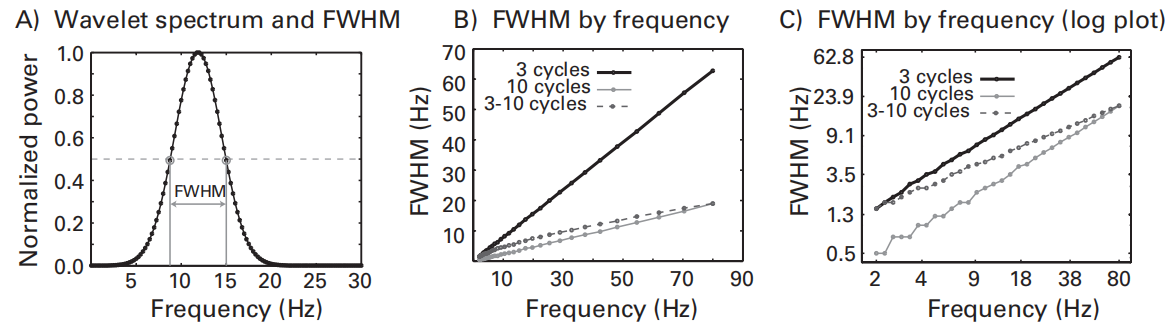
Full width at half-maximum (FWHM)
- 指频谱上功率在峰值的左右两侧分别为50%时的频率宽度： $FWHM=2\sqrt{2\ln 2}\sigma$ ，其中 $\sigma$ 是频率响应的标准差
  - 首先标准化功率谱，使得峰值为1，两端衰减至0
  - 找到功率值为0.5的点对应的频率，即可计算出FWHM

卷积的Matlab计算技巧

FFT的数据点数为 $2^n$ 时，计算速度更快。可以通过适当的补零来实现
不需要对每个trial进行一次卷积，可以将所有trial连接成一个长时间序列，再对整个时间序列执行一次卷积

14 | Bandpass Filtering and the Hilbert Transform

The Procedure of Hilbert Transform | Hilbert变换及其步骤

对于一个只有实部的信号 $A(t)\cos(2\pi ft)$ ，我们无法获得其相位信息，Hilbert变换能够帮助我们从实信号中提取出虚部，从而获得相位信息
正频率与负频率
- 正频率：介于0与奈奎斯特频率之间的频率（不包含0和奈奎斯特频率）
- 负频率：大于奈奎斯特频率
- 为什么要区分正频率与负频率？
  
  信号的实部与虚部：一个纯实信号（如 $M\cos⁡(2πft)$ ）在频域中有对称的正负频率分量，它们共同构成了这个信号的傅里叶表示。然而，虚部（如 $iM\sin ⁡(2πft)$ ）的引入使得信号不再是对称的，因此需要对正频率和负频率分量分别进行处理，以生成一个复信号。
Hilbert变换的步骤：
- 对信号做Fourier变换，得到 $M(t)\cos (2\pi ft)$ ，乘以复数单位 $i$ ，得到 $iM(t)cos(2\pi ft)$
- 正负频率的处理
  
  正频率的处理
  - 逆时针旋转四分之一周期：正频率分量的傅里叶系数在复平面上表示时，通过逆时针旋转四分之一周期（即 $-90°$ 或 $\frac{\pi}{2}$ ），可以将余弦信号（ $\cos ⁡(2πft)$ )转化为正弦信号（ $\sin⁡(2πft)$ ）。
  - 数学处理：这种旋转通过将傅里叶系数乘以 $−i$ （即$-i=e^{-i\pi/2}$）来实现。这样，当你把旋转后的正频率系数加回到原来的正频率系数时，实际操作效果是将这些系数变成了原来系数的两倍。
  负频率的处理
  - 顺时针旋转四分之一周期：负频率分量对应的傅里叶系数需要顺时针旋转四分之一周期（即$90°$或$\frac{\pi}{2}$），将余弦信号（$\cos ⁡(2πft)$）转化为负的正弦信号。
  - 数学处理：这个旋转通过将负频率傅里叶系数乘以 $i$ （即 $i=e^{i\pi /2}$ ）来实现。由于这导致$i$和$i$相乘等于-1，负频率的系数经过处理后在添加回原来的系数时会变成零。这意味着负频率部分被完全消除。

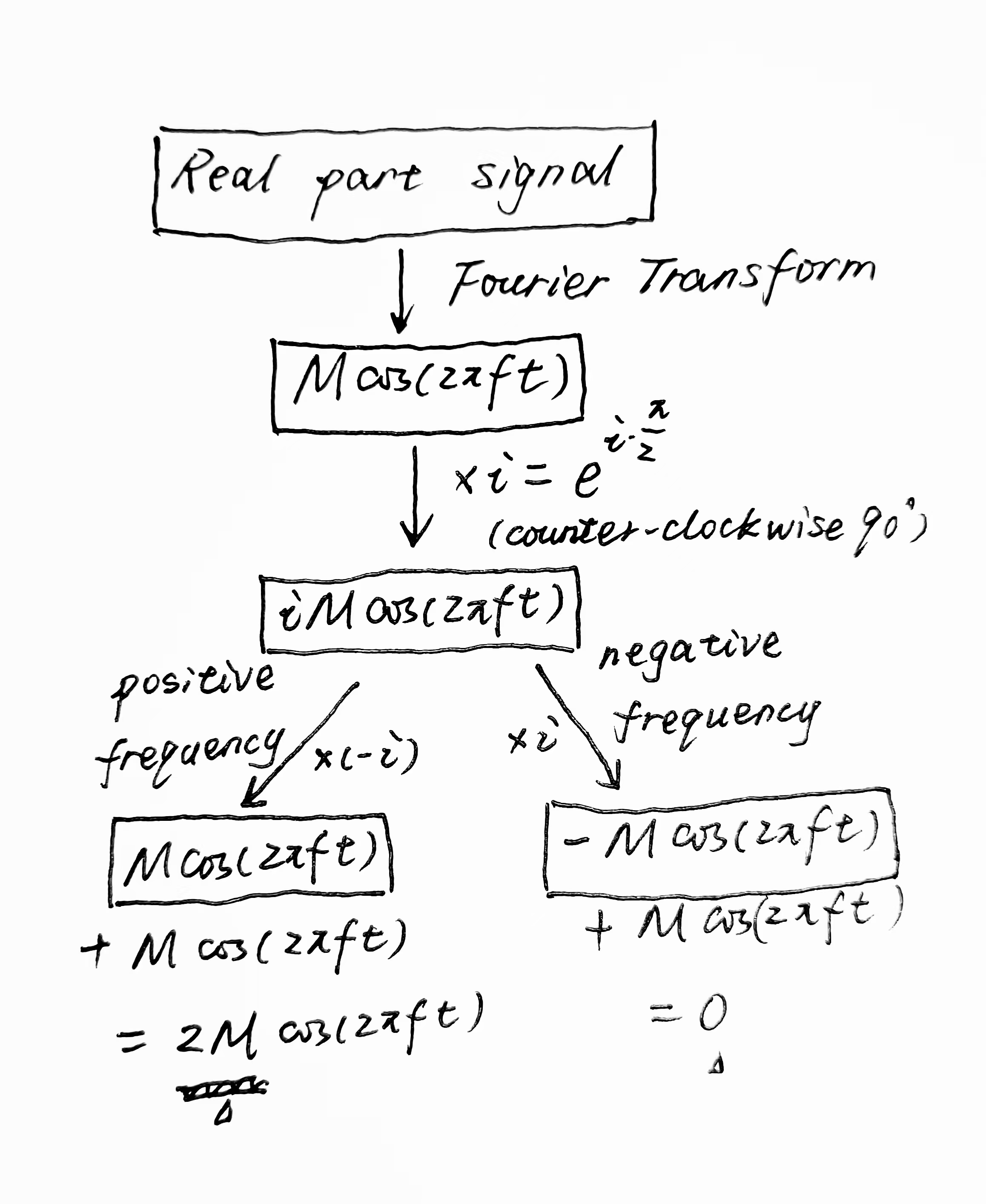
Hilbert变换的代码

%% the FFT-based hilbert transform

% generate random numbers
n = 21;
randomnumbers = randn(n,1);

% take FFT
f = fft(randomnumbers);
% create a copy that is multiplied by the complex operator
complexf = 1i*f;

% find indices of positive and negative frequencies
posF = 2:floor(n/2)+mod(n,2);	% 正频率：0到奈奎斯特频率
negF = ceil(n/2)+1+~mod(n,2):n;

% rotate Fourier coefficients
% (note 1: this works by computing the iAsin(2pft) component, i.e., the phase quadrature)
% (note 2: positive frequencies are rotated counter-clockwise; negative frequencies are rotated clockwise)
f(posF) = f(posF) + -1i*complexf(posF);
f(negF) = f(negF) +  1i*complexf(negF);
% The next two lines are an alternative and slightly faster method. 
% The book explains why this is equivalent to the previous two lines.
% f(posF) = f(posF)*2;
% f(negF) = f(negF)*0;

% take inverse FFT
hilbertx = ifft(f);

% compare with Matlab function hilbert
hilbertm = hilbert(randomnumbers);

Hilbert变换并不改变信号的实部，可用此性质检验变换后的信号是否正确
在Matlab中，函数hilbert()的输入可以是一个矩阵filtered_data = zeros(demension_1,demension_2)，但是矩阵的第一个维度必须是时间（filtered_data = zeros(EEG.pnts,EEG.nbchan)），即对于二维矩阵，矩阵的每一列是一组信号
在进行Hilbert变换前，建议先对信号进行滤波，从而将信号分离成不同的频段，以便于分析

Bandpass Filtering | 带通滤波

FIR & IIR Filters
- FIR (Finit Impluse Response, 有限冲激响应)：提供脉冲输入后，响应会在某一点终止。更稳定，且不容易引入非线性相位畸变
- FIR (Infinit Impluse Response, 无限冲激响应)：提供脉冲输入后，响应不会终止。算法计算复杂度更低，耗时少
Bandpass, Band-Stop, High-Pass, Low-Pass
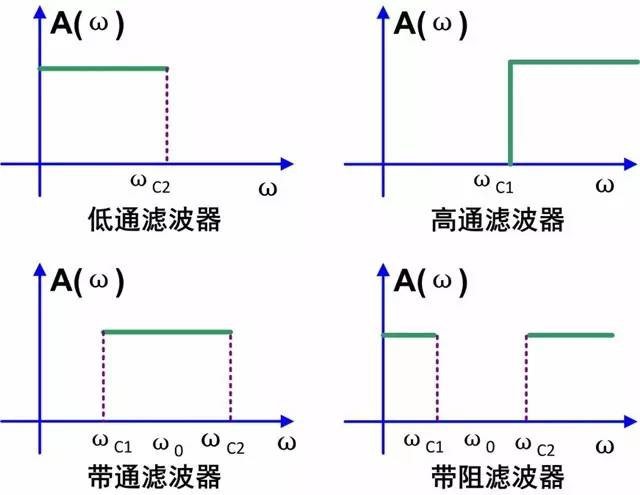
Create a filter kernel in Matlab
- firls()：通过最小二乘创建FIR滤波器。常用于宽频带
  - 第一个参数：The order of the filter，定义kernel的长度（单位为ms），决定了滤波器频率响应的精度。通常设置为下频界的2~5倍（如果下频界为10Hz（100ms），那么就是200到500ms）
  - 第二个参数：一个包含一组频率的频率向量，决定滤波器频率响应的形状。对于带通滤波器，可以使用六个频率：①零频率，②下过渡区开始的频率，③带通的下界，④带通的上界，⑤上过渡区结束的频率，⑥奈奎斯特频率。最后将这6个频率除以奈奎斯特频率（即以奈奎斯特频率为1）
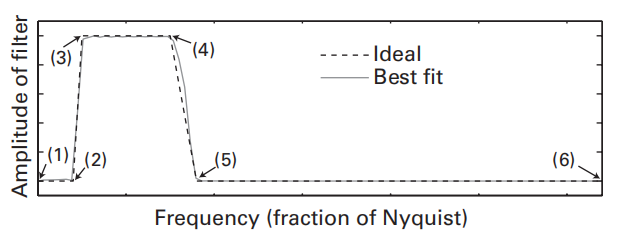
    - 第三个参数：一个元素为0~1的向量，通过控制第二个输入参数的纵坐标来修改滤波器频响形状。对于带通滤波器，可以使用[0 0 1 1 0 0]，其中的“1”对应带通平台的上下频界，第一个和最后一个“0”对应直流和奈奎斯特频率，第二个和第五个“0”对应过渡区的频率界。
- fir1()：带有紧密过渡区的窗函数线性相位滤波器。常用于窄频带
  - 第二个参数只需输入带通下界、带通上界两个频率值
- fir2()：基于频率采样的滤波器结构
- firrcos()：凸起的余弦形滤波器
- gaussfir()：高斯形滤波器
- firpm()：Parks-McClellan
频域内的尖锐边缘会引起时域内的伪影振荡，使用包含过渡区的滤波器可以缓解这一点，但是会牺牲一定的频率精度
检验滤波器是否合格：$sse=\Sigma_{i=1}^{n}(ideal_i-actual_i)^2$，sse即the sum of squared errors，对理想滤波器而言，n指的是滤波器的6个定位点（第二个参数）。
得到kernel后，使用filtfilt()函数完成对信号的滤波，该函数输入的第一个为kernel；第二个参数为一个标量和向量，代表kernel的权重。通常设为；第三个参数为被处理信号。
- 使用filter()函数会引入相位延迟，而filtfilt() 通过两次应用filter函数来消除相位延迟。具体来说，它首先对信号进行正向滤波，然后反转信号顺序，再次应用相同的滤波器，最后再将信号反转回来。

Butterworth (IIR) Filter

% 5th-order butterworth filter
[butterB,butterA] = butter(5,[(center_freq-filter_frequency_spread)/nyquist (center_freq+filter_frequency_spread)/nyquist],'bandpass');
butter_filter     = filtfilt(butterB,butterA,data2filter);

15 | Short-Time FFT

Short-Time FFT 即取一小段时间内的数据进行fft，为了减小artifact，需要对这一段数据的两侧进行减弱处理

可以用Hann、Hamming、Gaussian三种函数（tapers）完成减弱处理，推荐用Hann，因为它最终会衰减到0。其他taper还包括Kaiser, cosine, Blackman, …

timewin	= 400; % in ms, for stFFT
timewinidx = round(timewin/(1000/EEG.srate));

% create hamming
hamming_win = .54 - .46*cos(2*pi*(0:timewinidx-1)/(timewinidx-1));
% create hann
hann_win    = .5*(1-cos(2*pi*(0:timewinidx-1)/(timewinidx-1)));

% create gaussian
gaus_win = exp(-.5*(2.5*(-timewinidx/2:timewinidx/2-1)/(timewinidx/2)).^2);

得到FFT结果后，建议以目标频率周围几个频率的频响平均值（或Gaussian加权平均值）作为最终结果，可以提高信噪比

时间段长度的选择
- A trade-off between temporal and frequency precision and resolution
- 时间段长度应至少包含所分析频率的一个周期
- 时间段长度可以设为频率的函数（低频-时间段长；高频-时间段短）

16 | Multitapers

常用于低信噪比的情况，如高频活动或功率的单试次估计

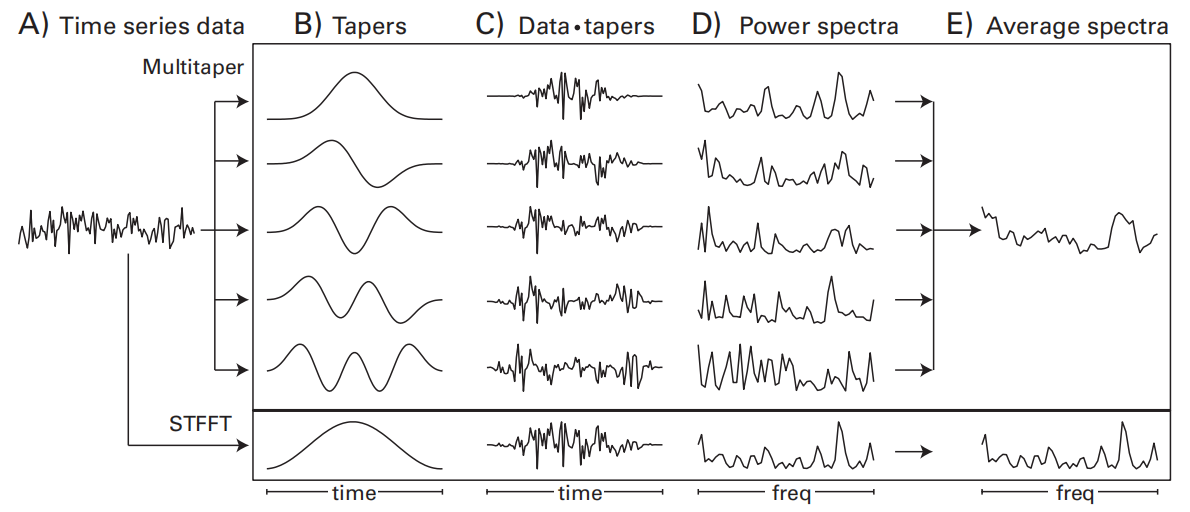
The Tapers

multitapers使用的tapers是discrete prolate spheroidal sequences，也叫做Slepian tapers。可以使用Matlab中的dpss()函数生成。一组slepian tapers相互正交

`dpss` 函数的基本调用格式如下：

[tapers, eigenvalues] = dpss(N, NW);

N：时间段的长度（以样本点为单位）。
NW：时间带宽参数。它是时间段长度和频带宽度的乘积，NW = N * (W / (Fs/2))，其中 W 是频带宽度（以采样率的一半为单位，所以要除以采样率的一半），Fs 是采样率。
tapers：返回的锥窗函数的矩阵，每一列是一个taper。
eigenvalues：对应的特征值，表示每个taper在指定频带内包含的能量。

确定参数

时间段长度 N：取决于你想要的时间分辨率。
带宽参数 NW：它控制频谱的平滑程度。NW 的值越大，频谱越平滑，但时间分辨率越低。通常，NW 的值在 2 到 4 之间，也可随频率值改变。

N = 1000; % 假设有1000个样本点
W = 2;    % 频带宽度, 以赫兹为单位
Fs = 1000; % 采样率

% 计算NW参数
NW = N * (W / (Fs/2));
[tapers, eigenvalues] = dpss(N, NW);

确定锥窗数量

dpss 函数返回的锥窗数量是 2*NW 四舍五入后的整数。

numTapers = round(2 * NW);

分析特征值

tapers 的最后一个特征值一般较低（例如 0.7 或 0.8），表示该taper的频谱表现较差，通常可以忽略这些较差的锥窗。

% 检查特征值
disp(eigenvalues);

% 忽略最后一个特征值较低的taper
tapersToUse = tapers(:, eigenvalues > 0.9);

5. 完整示例代码

% 参数设置
N = 1000; % 样本点数
W = 2;    % 频带宽度
Fs = 1000; % 采样率
NW = N * (W / (Fs/2));

% 生成tapers
[tapers, eigenvalues] = dpss(N, NW);

% 显示特征值
disp(eigenvalues);

% 选择特征值大于0.9的tapers
tapersToUse = tapers(:, eigenvalues > 0.9);

% 绘制tapers
figure;
plot(tapersToUse);
title('Selected DPSS Tapers');
xlabel('Time (samples)');
ylabel('Amplitude');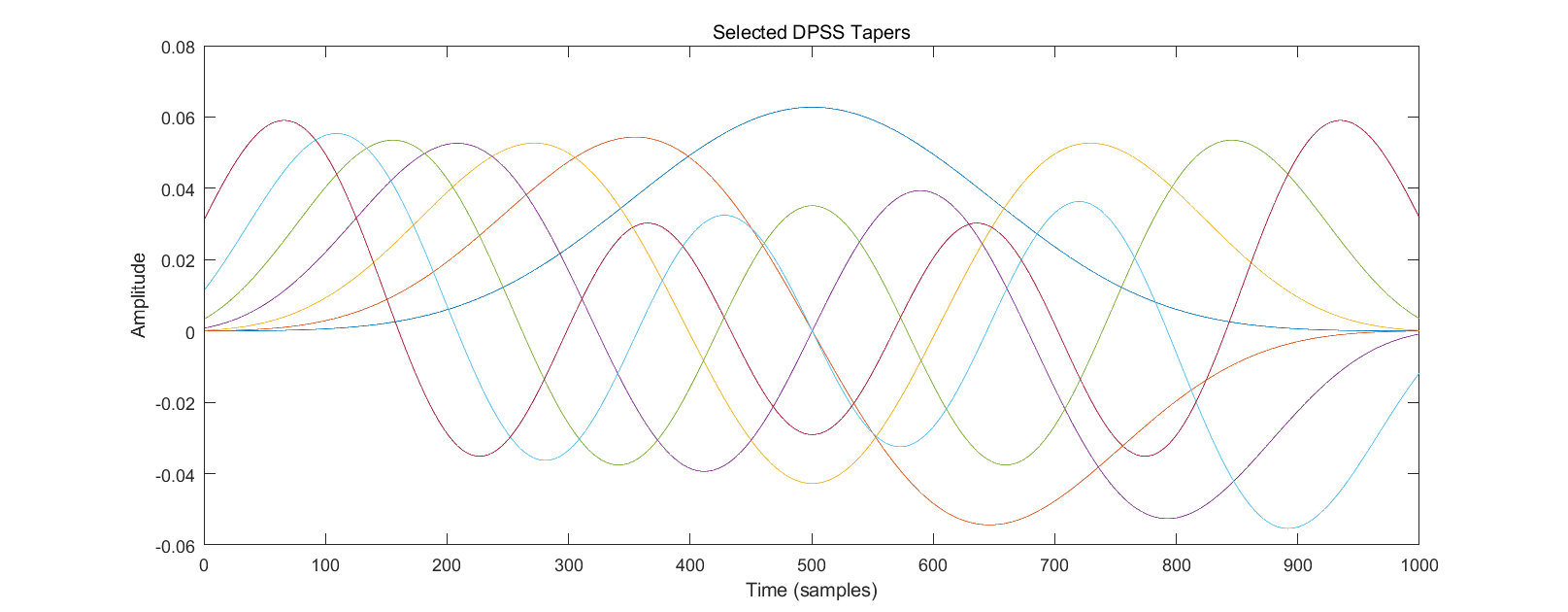

test_dps

通过使用多个taper，multitaper方法在频率轴上引入了一定的平滑效应。这种平滑可以减少频率分辨率的精细度，使得频谱变得更加连续和平滑。

（ChatGPT的例子）假设你在一个任务中研究Gamma频段活动，并且发现某些被试的伽马频段峰值在50Hz，而另一些被试的峰值在65Hz。如果你使用精细的小波分析，每个被试的频谱可能显示出各自独特的伽马活动峰值，但这些峰值的差异可能在跨被试平均时抵消，导致难以在群体水平上识别伽马活动。此时，通过使用multitapers方法并引入适当的频率平滑，你可以让50Hz和65Hz的峰值在频谱中更接近，从而在群体平均时更容易识别出Gamma频段的整体活动。这种平滑可以帮助你在不损失重要频率信息的情况下，更好地捕捉和解释群体层面的神经活动。
适用情况
- noisy data, small number of trials
- single-trial analyses, analyze frequencies above around 30 Hz
- high-frequency power above around 60 Hz

18 | Time-Frequency Power and Baseline Normalization

1/f Power Scaling

EEG的时频功率和频率呈现幂函数的关系：$power=\frac{c}{frequency^x}$，难以进行数据分析

Baseline

baseline指的是一段时间，通常在试验开始前几百毫秒，在这段时间内很少或没有任务相关的脑电活动。

Decibel Conversion

计算公式：

$dB_{tf}=10\log10(\frac{activity_{tf}}{\overline{baseline_f}})$

由于对数函数的存在，该公式不适用于存在非正值的数据，但功率值总是为正的。

Matlab计算代码

% 定义baseline所处时间段
baselinetime = [ -500 -200 ]; % in ms

% 找到baseline所划分时间段的时间索引
[~,baselineidx(1)]=min(abs(EEG.times-baselinetime(1)));
[~,baselineidx(2)]=min(abs(EEG.times-baselinetime(2)));

% dB-correct 转换为分贝指
baseline_power = mean(tf_data(:,baselineidx(1):baselineidx(2)),2);	% 以baseline时间段内功率的时间平均值作为baseline_power，即分贝计算的分母
dbconverted = 10*log10( bsxfun(@rdivide,tf_data,baseline_power));
% FYI: the following lines of code are equivalent to the previous line:
% dbconverted = 10*( bsxfun(@minus,log10(tf_data),log10(baseline_power)));
% dbconverted = 10*log10( tf_data ./ repmat(baseline_power,1,EEG.pnts) );
% dbconverted = 10*( log10(tf_data) - log10(repmat(baseline_power,1,EEG.pnts)) );

figure
contourf(EEG.times,frequencies,dbconverted,40,'linecolor','none')
set(gca,'ytick',round(logspace(log10(frequencies(1)),log10(frequencies(end)),10)*100)/100,'yscale','log','xlim',[-500 1500],'clim',[-12 12])

一些细节
- 对于多个trial平均后的数据，经分贝转换后的功率通常分布在$\pm 1-4\ dB$
- 通常采用对称的颜色映射分布，便于比较增大与减小的幅度。某些情况下也可以用不对称的分布来突出某些特征

Percentage Change

计算公式

$prctchange_{tf}=100\frac{activity_{tf}-\overline{baseline_f}}{\overline{baseline}_f}$

Baseline Division

计算公式 $BaselineDivision = \frac{activity_{tf}}{\overline{baseline_f}}$

Z-Transform

计算公式 $Z_{tf}=\frac{activity_{tf}-\overline{baseline_f}}{\sqrt{n^{-1}\sum_{i=1}^{n}(baseline_{if}-\overline{baseline_f})^2}}$ 其中n是baseline中的时间点数目，分母是baseline的标准差。当baseline的标准差较大时，不建议使用Z-Tranform

均值or中位数

在trial数量少、噪声大的情况下，中位数更不易受到离群值的影响
在对所有trial进行平均前，先对单个trial进行baseline normalization（single-trial Z-transform），可以减少离群数据的影响

如何选择Baseline

ERP
- baseline通常终止于time=0
time-frequency analyses
- baseline通常设置为 -500 ~ -200 ms 或 -400 ~ -100 ms。因为在提取频域信息时，每个时间点上的数据会“泄露”到周围的时间点上，所以应该尽量避开刺激前的一段时间
- 要确保选择的baseline时间段内没有多余的刺激，比如试验开始的提示等
- 尽可能使用pretrial period作为baseline，而非preresponse period等其他时间段，以减少刺激相关神经活动的影响
- baseline通常包含几百毫秒
- 如果无法使用pretrial period作为baseline，可以考虑如下替代方案
  - 使用休息时间作为baseline。但被试对待休息与试验时心态的差异可能会影响最终结果
  - 使用对照条件（区别于实验条件）作为baseline。对照与实验条件下反应时间的差异可能会影响最终结果
  - 使用整个实验过程作为baseline。难以观测到功率在整个实验中的持续变化
- 如果有多种不同的试验条件（condition），需要考虑使用 condition-specific baseline 还是 condition-average baseline ，即不同条件是否要使用同一段baseline

Signal-to-Noise Ratio (SNR) Estimates| 信噪比的估计

信噪比：可以认为是信号的平均值与信号的标准差的比值
计算公式：
$SNR=\frac{\mu}{\sigma}$
对ERP而言
- $\mu$可以认为是某个ERP成分的峰值，$\sigma$可以认为是baseline的时间方差
对time-frequency analyses
- $SNR_{tf}$：$\mu$为所有trial的平均功率，$\sigma$为所有trial的功率标准差，$tf$表示一个时频点
- $SNR_{base}$：$\mu$为所有trial的平均功率，$\sigma$为baseline的功率标准差

检验Trial的数量是否足够

随机选取n个trial，计算这n个trial的平均值与所有trial平均值的相关系数，相关性越强，说明trial的数目越充足。对于没有进行baseline transform的非正态分布数据，通常计算Spearman相关系数

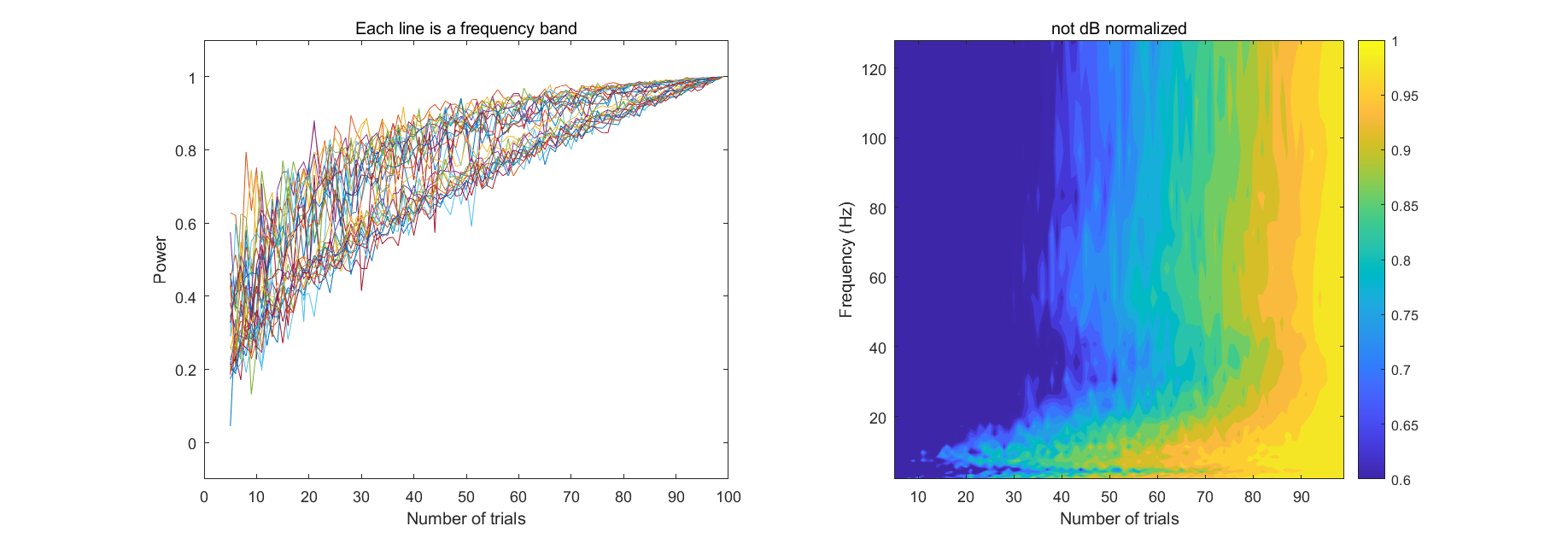
Figure18.13

DownSampling | 降采样

时频分解后由于泄露，信号的时间精度会降低，因此时间分辨率可以适当降低，比如降低到 40 或 50 Hz

19 | Intertrial Phase Clustering

Intertrial Phase Clustering (ITPC)

主要思路：将不同trial在某一时刻的相位向量绘制在复平面上，模长为1，角度为各相位值，再计算所有向量的平均值，所得新向量的平均长度介于0和1之间，反映了多个Trial间相位的一致性(ITPC)，新向量的相位角则反映了相位的平均大小
计算公式：
$ITPC_{tf}=|n^{-1}\Sigma^n_{r=1}e^{ik_{tfr}}|$

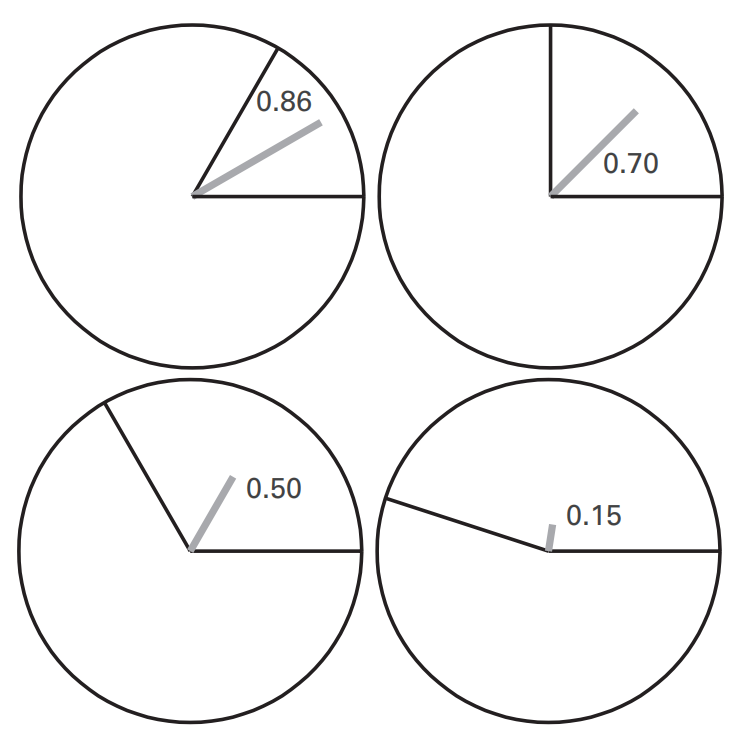
Trial数目越多，ITPC值减小并趋于稳定。所以尽量保证Trial数目足够多，且不同实验条件下的Trial数尽量保持一致
Trial数目不足且不一致时可采用的措施
- 对trial进行筛选，以匹配不同条件下的trial数目
- 采用baseline ITPC，因为不服从1/f的分布，通常采用linear baseline
- 将$ITPC$转换为$ITPC_Z$
  $ITPC_Z=n\cdot ITPC^2$

Effect of Temporal Jitter on ITPC

Temporal Jitter：刺激呈现等事件发生时间的波动或不确定性
Temporal Jitter对相位的影响大于对功率的影响，且在高频处的影响更大

ITPC and Power

ITPC和Power通常是不相关的，可以分别进行分析说明
功率越小，相位越难估计（可以想象功率为0的极端情况）

Weighted ITPC (wITPC)

wITPC中向量的长度不是1，而是和试验中的行为或试验变量有关，比如反应时间、刺激亮度、瞳孔反映等

$wITPC_{tf}=|n^{-1}\Sigma^n_{r=1}b_re^{ik_{tfr}}|$

wITPCz（待补充）

20 | Differences among Total, Phase-Locked, and Non-Phase-Locked Power and Intertrial Phase Consistency

Non-Phase-Locked Power (Induced Power)
- 计算方法：首先从每次试验的数据中减去ERP，然后对单次试验进行时间-频率分解，计算功率。这种方法去除了所有相位锁定的成分，因此剩下的功率仅代表非相位锁定的部分
Phase-Locked Power
- 计算方法：从总功率中减去非相位锁定功率，注意需要先将总功率和非锁相功率分别转化为分贝，再相减
- 高频活动在多个周期后难以保持相位锁定，因此相位锁定功率中通常不包含大于20Hz左右的高频成分
ERP Time-Frequency Power
- 先计算ERP，再进行频域变换，而不是先进行频域变换，再计算ERP
- It is appropriate to use the ERP baseline to normalize the ERP time-frequency power, rather than using the base line period power from the total or non-phase-locked analysis.

22 | Surface Laplacian

概述

采用Surface Laplacian可以突出局部的空间特征，削弱空间上广泛分布的活动
“Surface Laplacian” 和 “Current Scalp Dencity” 的区别
- Surface Laplacian 只是一种空间滤波的方法
- Current Scalp Dencity 强调滤波后的结果
Surface Laplacian只能用于EEG（不能用于MEG），且通常用于电极数目大于64的EEG数据
The Laplacian is more sensitive to radial dipoles than it is to tangential dipoles.
Activity seen in the surface Laplacian is dominated (although not necessarily entirely driven) by radial dipoles in regions of the cortex close to the skull (such as gyral crowns).
The Laplacian must be applied to time-domain data, not to time-frequency data.

公式

The weights that are applied to the data such that the activity at each electrode becomes a weighted sum of activity of all other electrodes.

$G_{ij}=(4\pi)^{-1}\sum^{order}_{n=1}\frac{(2n+1)P_n(cosdist_{ij})}{(n(n+1))^m}$ $H_{ij}=(4\pi)^{-1}\sum^{order}_{n=1}\frac{-2(n+1)P_n(cosdist_{ij})}{(n(n+1))^{m-1}}$

The cosine distance among all pairs of electrodes

$cosdist_{ij}=1-\frac{(X_i-X_j)^2+(Y_i-Y_j)^2+(Z_i-Z_j)^2}{2}$

The Laplacian for electrode i at one time point

$lap_i=\sum^{nelec}_{j=1}C_iH_{ij}$

The C matrix is where the data are finally introduced

$C_i=d_i-\frac{\sum^{nelec}_{j=1}d_j}{\sum^{nelec}_{j=1}Gs_j^{-1}}Gs^{-1}$ $d_i=data_j^{-1}Gs$ $Gs=G+\lambda$

Surface Laplacian for Connectivity Analyses

经过Surface Laplacian的处理后，电极间信号的相关性与电极距离的联系减弱，但间隔比较近的电极仍然会相互影响，因此应该避免对间隔5cm以内的电极采用空间相关性的规律解释。

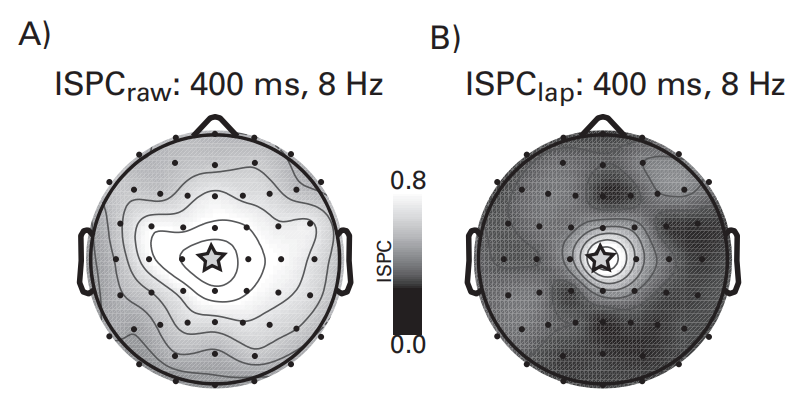
23 | Principal Components Analyses (PCA)

用最直观的方式告诉你：什么是主成分分析PCA

概述

与 Surface Laplacian 相反，PCA反映的不是电极的局部特征，而是弱化局部特征后的总体特征

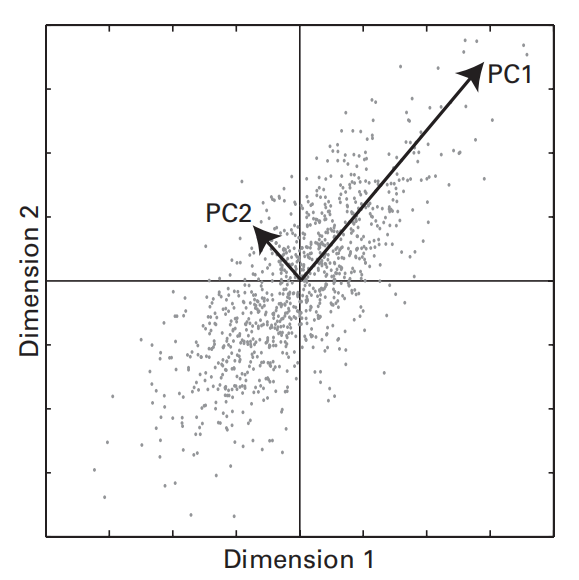
公式

计算协方差

协方差的矩阵计算公式:

$covariance = (n-1)^{-1}(X-\bar{X})(X-\bar{X})^T$

如果把电极作为变量，电极数目为变量的维度，每一个时间点下各个电极的数据看作一次观测得到的结果，组成一个列向量，那么经过多个时间点的观测后，我们可以得到一个 $electrodes(m) \times time\ points(n)$ 的矩阵$X$：

$X=\begin{bmatrix} d_{e_1t_1} & d_{e_1t_2} & \cdots & d_{e_1t_n}\\ d_{e_2t_1} & d_{e_2t_2} & \cdots & d_{e_2t_n}\\ \vdots & \vdots & \ddots & \vdots\\ d_{e_mt_1} & d_{e_mt_2} & \cdots & d_{e_mt_n} \end{bmatrix}$

协方差公式中的$\bar{X}$是各列向量的平均值，即关于时间点的平均值，n是时间点的数目。协方差矩阵的对角线元素则为对应维度的方差

对于多个试次的数据，可以采用三种方式计算协方差：

先计算ERP，再以ERP作为各数据值得到矩阵$X$。该计算方法得到的是phase-locked (evoked) covariance
将各试次作为不同的观测点，得到的$X$矩阵有$electrode$行，$time\ points \times trials$列，进一步以此矩阵计算协方差。得到的是total (phase-locked and non-phase-locked) covariance
（常用）先对每一个试次计算协方差，最后平均。该方法可以提高信噪比，得到的是total (phase-locked and non-phase-locked) covariance

计算协方差矩阵的特征值和特征向量

采用matlab中的eig或svd函数计算协方差矩阵的特征值和特征向量。注意，Matlab函数eig以升序返回特征值和特征向量，但是让结果按降序排序会更直观。

特征向量是旋转后的坐标轴方向
特征值是旋转后坐标轴的长度，经归一化可后作为对应主成分的百分比方差，即对每个特征值除以所有特征值的和，再乘以100

特征向量矩阵中的每一列都是一个主成分，该列的每行元素存储对应电极的权重（weight），通常权重的正负符号不重要

结果的呈现与解释说明

PCA map：特征向量矩阵每一列可由topoplot绘制成一张PCA map图
time course：将每个时间点下的各电极权重（特征向量中的一行）与电极对应的时间序列数据（$X_i-\bar{X_i}$）相乘，再相加，得到一个时间点下的time course。每一个主成分（每一列）对应一个权重，也就对应一组time course（即各电极的加权和）。得到主成分时间序列数据（time course）后，可以对这些数据采用与其他时间序列数据相同的方法进行分析，比如计算ERP或时频功率等。
可以根据特征值的大小对主成分进行取舍
可以计算所有特征值比阈值低的成分对应的方差，以估计全局脑电图响应的“噪声”
特征值下降的快慢可以理解为系统的复杂度的大小，下降得越快，被舍弃的成分越多，系统的复杂度越小

Independent Components Analysis（ICA）

PCA和ICA的区别

PCA的作用：去相关性、降维
ICA的作用：分离独立源

24 | Single-Dipole and Distributed-Source Imaging

Forward Solution & Inverse Problem

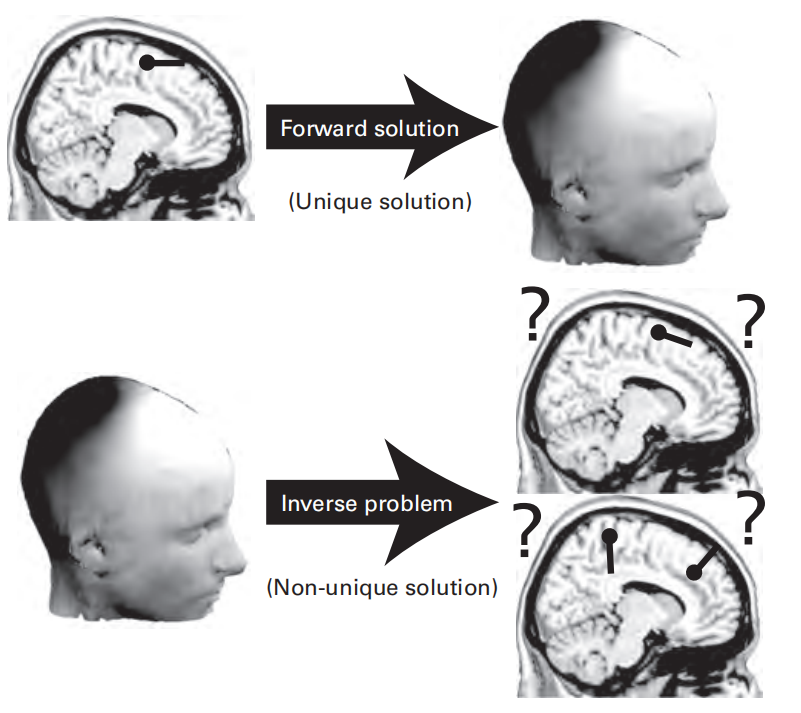
Inverse Problem

Dipole Fitting：需要确定偶极子（dipole）的位置、方向、大小
Distributed-Source Imaging：已经确定了偶极子的位置和方向，只需要确定大小
you should be cautious when hearing claims of functional-anatomical dissociations of less than a few centimeters based on results of source reconstruction. Such high spatial accuracy is possible but not common.

25 | Introduction to the Various Connectivity Analyses

Connectivity：指在同一时刻下考虑多个信号之间关系的分析。
需区分的概念：
- functional connectivity：linear or nonlinear covariation between fluctuations in activity recorded from distinct neural networks. 更接近于相关性（correlation）
- effective connectivity：a causal influence of activity in one neural network over activity in another neural network. 更接近于因果关系（causation）
两个电极之间的功能连接（connectivity）可以反映不同大脑区域之间的真实连接，也可能是由于这两个电极测量了来自同一脑源的活动。

26 | Phase-Based Connectivity

ISPC (Intersite phase clustering)

ISPC是一种用以描述基于相位的功能连接的方法，与ITPC相似，但计算的是两电极之间随时间或试次变化的相位角差的平均值

$ISPC_f=|n^{-1}\sum^n_{t=1}e^{i(\phi_{xt}-\phi_{yt})}|$

其中 n 是时间点数目或试次数目，$\phi_x$ 和 $\phi_{y}$ 是电极 x 和 y 在频率f下的相角，t是时间点或试次。

ISPC反映的不是两电极相位差的大小，而是相位差随时间或试次的一致性
ISPC是无向的（A→B的ISPC和B→A的相同）

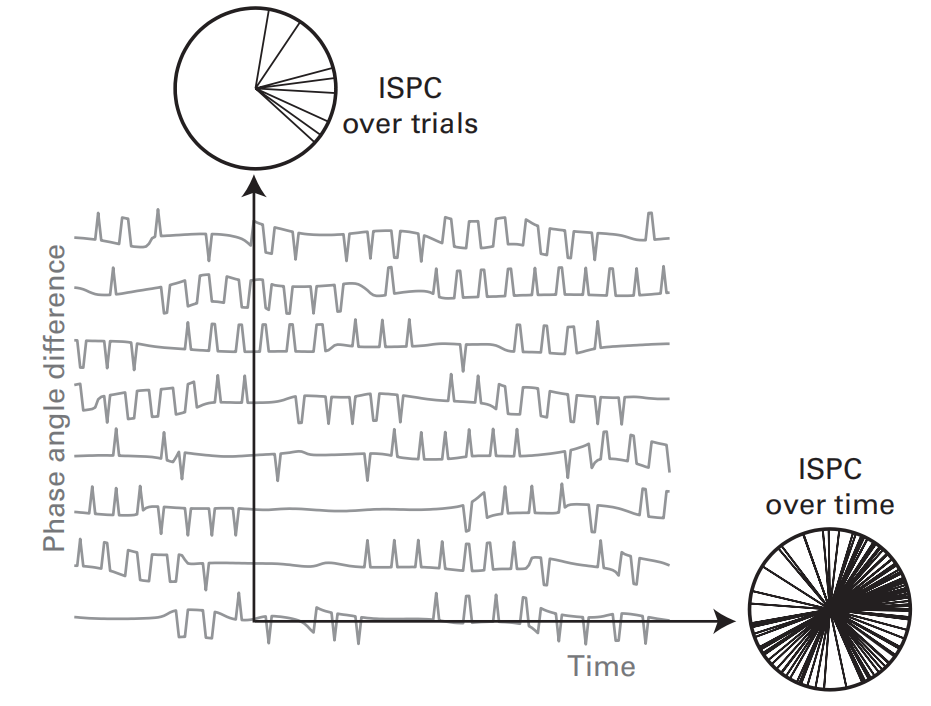
ISPC-time and ISPC-trial

通过上面的公式，我们可以得到的是在一个时间窗口内一个试次的ISPC，如果有多个试次，而且我们想要得到ISPC随时间/试次的变化，可以采用如下方法：

ISPC-time：设置一个滑动的小时间窗，计算单个试次在每个时间窗下的ISPC（类似于short-time FFT），得到多个试次下的ISPC随时间的变化，最后再进行试次平均，得到ISPC在不同时刻下的值。小时间窗的长度选取规则类似于wavelet中the number of cycles的选取。
ISPC-trials：关注某一时间点下不同试次的相位差大小。ISPC-trial所反映是在不同的试次下，两电极间的相位差是否能保持一致，其值越大，说明相位差在不同试次下越能保持一致。
- 对试次的数目比较敏感，试次数目需要足够多，才能获得稳定的结果
- 如果在不同实验条件下的试次不同，可以考虑使用 weighted ISPC-trials (wISPC-trials)，其原理与 wITPC 相近。
计算时的区别：
- ISPC-time：先在滑动时间窗内时间平均，最后试次平均
- ISPC-trial：在不同时间点下进行试次平均

Matlab代码实现：

% 对于频率，通常采用对数分布
freqs2use  = logspace(log10(4),log10(30),15); % 4-30 Hz in 15 steps
% 非频率值，可以采用线性分布，timewindow的宽度是下面取值的两倍
timewindow = linspace(1.5,3,length(freqs2use)); % number of cycles on either end of the center point (1.5 means a total of 3 cycles))

ISPC-time (ispc) 和 ISPC-trial (ps) 的计算：

for fi=1:length(freqs2use)
    % phase angle differences（维度为time×trials）
    phase_diffs = phase_sig1-phase_sig2;
    
    % compute ISPC over trials（trial平均，时间没有平均，所以ps的是"频率×时间"的矩阵）
    ps(fi,:) = abs(mean(exp(1i*phase_diffs(times2saveidx,:)),2));
    
    % 计算每一个时间点（timewindow中点）下的ISPC
    for ti=1:length(times2save)
        
        % compute phase synchronization（ISPC-time，每个时间窗可计算出一个值，1×trial）
        phasesynch = abs(mean(exp(1i*phase_diffs(times2saveidx(ti)-time_window_idx:times2saveidx(ti)+time_window_idx,:)),1));
        
        % average over trials（trial平均）
        ispc(fi,ti) = mean(phasesynch);
    end
end % end frequency loop

最后可以让每个时间点减去baseline时间内的ISPC平均值，突出任务相关影响：

% ISPC-time
contourf(times2save,freqs2use,ispc-repmat(mean(ispc(:,baselineidx(1):baselineidx(2)),2),1,size(ispc,2)),20,'linecolor','none')

% ISPC-trial
contourf(times2save,freqs2use,bsxfun(@minus,ps,mean(ps(:,baselineidx(1):baselineidx(2)),2)),20,'linecolor','none')

Spectral Coherence (Magnitude-Squared Coherence) | 波谱相干

波谱相干可以理解为是把信号功率作为权重的加权ISPC

公式

常见的波谱相干公式：=

$Coher_{xy}=\left| \frac{S_{xy}}{S_{xx}S_{yy}}\right|$

$S_{xy}$ 是电极x和y处的互功率谱密度，$S_{xx}$ 和 $S_{yy}$ 是电极x和y处的自功率谱密度。上式中的分子有时会平方，从而和分母的量级相配合。

为便于理解，可以将波谱相干公式写成下面的形式：

$C_{xy}=\left| n^{-1}\sum^n_{t=1}\lvert m_{tx}m_{ty}\rvert e^{i\phi_{txy}}\right|^{2}$

$m_x$和$m_y$是解析信号（没有负频率分量的复值函数）X和Y的功率大小（magnitudes），$\phi_{xy}$是电极X和Y之间的相位角差，t指trial或时间点。

可以发现使用这一公式计算出的$C_{xy}$值会随着功率大小改变，而功率又会随频率、时间、任务等改变，所以可以将这一公式进行归一化，得到如下波谱相干公式：

$Coher_{xy}=\frac{C_{xy}}{\left(n^{-1}\sum^n_{t=1}|m_{tx}|^2\right)\left(n^{-1}\sum^n_{t=1}|m_{ty}|^2\right)}$

由这种方法得到的波谱相干性大小将介于0和1之间，1代表完全相干，0代表完全独立。

Matlab代码实现

计算自功率谱大小时，使用信号乘以其共轭的方法 sig1.*conj(sig1)，耗时比直接平方(sig1).^2更短
计算互功率谱$S_{xy}$时，使用信号1乘以信号2的共轭的方法sig1.*conj(sig2)，耗时比欧拉公式abs(sig1).*abs(sig2).*exp(1i*(angle(sig1)-angle(sig2)))更短

% select channels
channel1 = 'fz';
channel2 = 'o1';

% wavelet and FFT parameters
time          = -1:1/EEG.srate:1;
half_wavelet  = (length(time)-1)/2;
n_wavelet     = length(time);
n_data        = EEG.pnts*EEG.trials;       
n_convolution = n_wavelet+n_data-1;

chanidx    = zeros(1,2); % always initialize!
chanidx(1) = find(strcmpi(channel1,{EEG.chanlocs.labels}));
chanidx(2) = find(strcmpi(channel2,{EEG.chanlocs.labels}));

% data FFTs （把一个电极里所有trial的数据排列成一个行向量，减少计算的次数）
data_fft1 = fft(reshape(EEG.data(chanidx(1),:,:),1,n_data),n_convolution);
data_fft2 = fft(reshape(EEG.data(chanidx(2),:,:),1,n_data),n_convolution);


% initialize
spectcoher = zeros(length(freqs2use),length(times2save));

for fi=1:length(freqs2use)
    
    % create wavelet and take FFT
    s = num_cycles(fi)/(2*pi*freqs2use(fi));
    wavelet_fft = fft( exp(2*1i*pi*freqs2use(fi).*time) .* exp(-time.^2./(2*(s^2))) ,n_convolution);
    
    % phase angles from channel 1 via convolution
    convolution_result_fft = ifft(wavelet_fft.*data_fft1,n_convolution);
    convolution_result_fft = convolution_result_fft(half_wavelet+1:end-half_wavelet);
    % 把原来排成一行的结果变回 electrodes×trials
    sig1 = reshape(convolution_result_fft,EEG.pnts,EEG.trials);
    
    % phase angles from channel 2 via convolution
    convolution_result_fft = ifft(wavelet_fft.*data_fft2,n_convolution);
    convolution_result_fft = convolution_result_fft(half_wavelet+1:end-half_wavelet);
    % 把原来排成一行的结果变回 electrodes×trials
    sig2 = reshape(convolution_result_fft,EEG.pnts,EEG.trials);
    
    % compute power and cross-spectral power
    % 自功率谱
    spec1 = mean(sig1.*conj(sig1),2);
    spec2 = mean(sig2.*conj(sig2),2);
    % 交叉功率谱的平方
    specX = abs(mean(sig1.*conj(sig2),2)).^2;
    
    % alternative notation for the same procedure, using the Euler-like expression: Me^ik
    %spec1 = mean(abs(sig1).^2,2);
    %spec2 = mean(abs(sig2).^2,2);
    %specX = abs(mean( abs(sig1).*abs(sig2) .* exp(1i*(angle(sig1)-angle(sig2))) ,2)).^2;

    % 计算Coherence。compute spectral coherence, using only requested time points
    spectcoher(fi,:) = specX(times2saveidx)./(spec1(times2saveidx).*spec2(times2saveidx));
    
    % yet another equivalent notation, just FYI
    %spec1 = sum(sig1.*conj(sig1),2);
    %spec2 = sum(sig2.*conj(sig2),2);
    %specX = sum(sig1.*conj(sig2),2);
    %spectcoher(fi,:) = abs(specX(times2saveidx)./sqrt(spec1(times2saveidx).*spec2(times2saveidx))).^2;
   
end

最终的结果可以减去baseline时间段的coherence：

contourf(times2save,freqs2use,spectcoher-repmat(mean(spectcoher(:,baselineidx(1):baselineidx(2)),2),1,size(spectcoher,2)),20,'linecolor','none')

Phase Lag-Based Measures

spurious connectivity results that are caused by two electrodes measuring activity from the same source will have phase lags of zero or $\pi$ ( $\pi$ if the electrodes are on opposite sides of the dipole). 由体积传导（同源）引起的相位差通常为0或$\pi$。

Imaginary Coherence

Imaginary coherence uses almost the same equation as that for spectual coherence, except the imaginary part of te spectual coherence is taken before the magnitude.

% imaginary coherence
    spec1 = sum(sig1.*conj(sig1),2); %imaginart
    spec2 = sum(sig2.*conj(sig2),2);
    specX = sum(sig1.*conj(sig2),2);
    spectcoher(fi,:) = abs(imag(specX(times2saveidx)./sqrt(spec1(times2saveidx).*spec2(times2saveidx))));

Phase-Lag Index（PLI）

根据上面的结论，我们可以有一个感性的认识：由体积传导引起的相位差通常分布在极坐标的0或$\pi$附近（关于实轴对称，指向左右），而不含体积传导的相位差将会分布在虚轴的正半轴或负半轴附近（关于虚轴对称，指向上下）。

The Phase-lag index（PLI）就通过计算互功率谱密度的虚部符号平均值，来定量地描述相位信号受体积传导效应影响的大小：

$PLI_{xy}=\left| n^{-1}\sum^n_{i=1}sgn(imag(S_{xyt})) \right|$

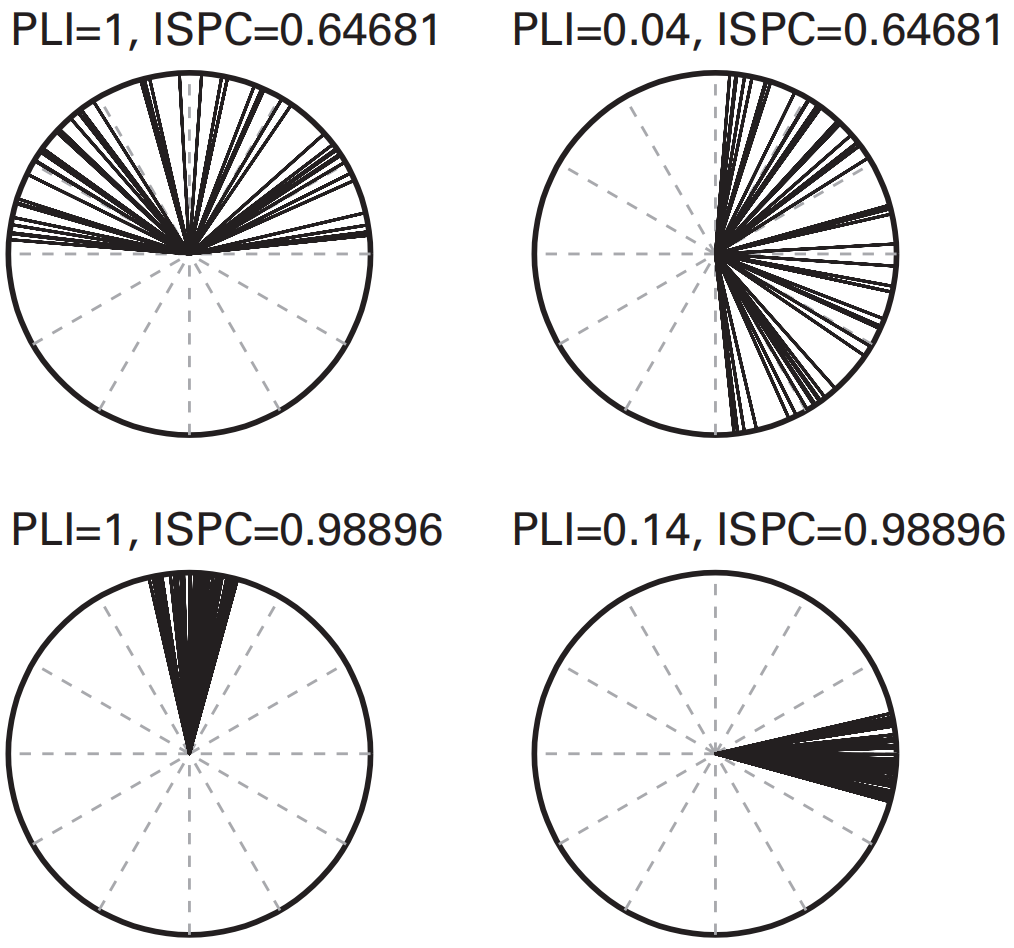
The weighted phase-lag index（wPLI）通过添加一个权重，使得离虚轴越近（虚部越大）的互功率谱密度值对PLI的贡献更大：

$PLI_{xy}=\frac{n^{-1} \sum^n_{i=1}\left|imag(S_{xyt}) \right|sgn(imag(S_{xyt}))}{n^{-1} \sum^n_{i=1}\left|imag(S_{xyt}) \right|}$

The phase-slope index

略

Mean Phase Angle

在前文的计算中，我们关注的是计算得的connectivity（平均相位差向量/ISPC）的长度，以此来表征相位差的随时间或试次集中程度。实际上，平均相位差向量的相角（mean phase angle）也值得关注：

它反映了两个电极之间的平均相位差
可以测试相角或相角差是否在某些指定的相角上存在显著差异。这可以用于检测体积传导对结果造成的污染，也可以用于测试首选相位角是否对Connectivity的计算结果（不太理解）
$u=nISPC\cos{(\phi-\Phi)}\sqrt{\frac{2}{n}}$
其中n是试次数目或时间点数目，$\phi$是测得的相角差，$\Phi$是要检验的假设相位角。

在数据点数目大的情况下，v-test 容易产生假阳性并具有对称性问题。为克服这些局限性，gv-test（Gaussian v-test）通过用高斯函数替代余弦成分，改进了对大量数据点的处理，减少了假阳性，并更精确地针对特定相位区域进行检验。

在计算出ISPC后，可以用gv-test以检验该结果是否受体积传导影响。如果gv-test提供了相位角差为0或$\pi$的证据，结果可能表明相位差为0、$\pi$或数据受体积传导污染。

27 | Power-Based Connectivity

Pearson versus Spearman Coefficient

1. Pearson 相关系数

公式

$r=\frac{\sum^n_{t=1}(x_t-\bar{x})(y_t-\bar{y})}{\sqrt{\sum^n_{t=1}(x_t-\bar{x})^2\sum^n_{t=1}(y_t-\bar{y})^2}}$

矩阵形式

当x、y是行向量时

$r=\frac{x_1y_1^T}{\sqrt{(x_1x_1^T)(y_1y_1^T)}}$

其中$x_1$、$y_1$是矩阵x、y的每行分别减去其对应的行均值后的结果

当x、y是 electrode×time 矩阵时

$r=\frac{x_1y_1^T}{\sqrt{diag(x_1x_1^T)diag(y_1y_1^T)^T}}$

其中的分数线表示分子分母矩阵对应按元素相除，该公式计算的是数据x、y行与行之间的相关系数

matlab代码实现：

% a、b中的每行代表一个电极上的数据
a = randn(4,100);
b = randn(4,100);

a1=a-mean(a,2);
b1=b-mean(b,2);
c = [a; b];

% 使用Matlab自带函数corrcoef和corr 
corr1 = corrcoef(c');
% corrcoef计算结果为8×8的矩阵，其中包含a、b与自身各行间的相关系数，将这一部分舍去
corr1 = corr1(1:4,5:8);
% corr函数计算结果为4×4的矩阵
corr2 = corr(a',b','type','p');

% 使用Pearson相关系数公式
corr3 = zeros(4,4);
for i = 1:4
    for j = 1:4
        corr3(i,j) = (a1(i,:)*b1(j,:)')/sqrt( (a1(i,:)*a1(i,:)')*(b1(j,:)*b1(j,:)') );
    end
end

% Pearson公式矩阵计算
corr4 = a1*b1'./sqrt(diag(a1*a1')*diag(b1*b1')');

其他说明

对Pearson相关系数结果的解释说明建立在数据是正态分布的假设前提上

2. Spearman相关系数

将Pearson公式中x、y元素的值替换成它们在各自向量中对应的从小到大排列顺序，计算后得到的即为Spearman系数。

在Matlab中，获取从小到大排列顺序可以由tiedrank实现。例如：对 [10 20 30 40 20] 从最小值到最大值进行计数，两个 20 值分别是第 2 个和第 3 个，因此它们都得到秩 2.5（2 和 3 的平均值）

tiedrank([10 20 30 40 20])
ans =
    1.0000    2.5000    4.0000    5.0000    2.5000

3. 两种相关系数的适用场景

当数据不是正态分布或是存在离群值时，应该使用Spearman相关系数，如果数据正态分布其没有离群值，那么两种相关系数的计算结果相近。而实际的EEG中，time-frequency 功率数据不是正态分布的（见Chap.18），所以通常采用Spearman相关系数。
经过baseline-averaged（decibel or percentage change）以及trial averaged的功率数据通常是正态分布的，可以使用Pearson相关系数进行分析。例如一些跨被试的实验分析。

4. Fisher-Z transform

相关系数的计算结果 r 在 [-1,1] 之间分布，可以通过 Fisher-Z transform 转化为近似正态分布：

$r_{fz}=0.5\times\log(\frac{1+r}{1-r})$

Fisher-Z transform实际上是双曲函数tanh的反函数atanh。

Power Correlations over Time

1. 计算步骤

选择两个电极，对数据进行时频提取
选择要计算的时间段和频带（time-frequency window），两电极的频带不一定要相同
计算两个电极在该时间段、频带内功率数据的相关系数
时间段的选取：
- 过长无法检测到瞬态变化
- 过短数据点太少，结果鲁棒性不强
- 至少要比所选频段的一个周期更长
- 对任务相关的数据，至少需要2-4个周期
- 对静息状态的数据，为提高信噪比，可以将数据分成几个互不重叠的几秒的时间段，分别计算相关系数，最后再平均

Cross-correlation | 互相关

在互相关的计算中，将一个时间序列相对于另一个时间序列进行时间偏移（时移的长度不能大于一个周期），每次时移重复计算一次相关系数，观察是否相关系数存在一个峰值。

可以通过Matlab中xcov的coeff选项实现，但该函数计算的不是Spearman相关系数，所以使用前要先用tiedrank函数对输入数据进行排序

% Compute how many time points are in one cycle, and limit xcov to this lag
nlags = round(EEG.srate/centerfreq);

% 使用前先用`tiedrank`函数进行排序
% note that data are first tiedrank'ed, which results in a Spearman rho
% instead of a Pearson r. 
[corrvals,corrlags] = xcov(tiedrank(abs(convolution_result_fft1(:,trial2plot)).^2),tiedrank(abs(convolution_result_fft2(:,trial2plot)).^2),nlags,'coeff');

% convert correlation lags from indices to time in ms
corrlags = corrlags * 1000/EEG.srate;

Power Correlation over Trials

1. 方法一

选择两个电极，分别对每个电极选择要计算的时间段和频带，所选择的时频区间不一定要相同
提取所需时频区间的信号功率，然后对于每一个试次，计算时频区间内的所有功率的平均值，得到一个数值
最后计算两个电极所有试次对应数值间的相关系数

2. 方法二

选择两个电极，分别对每个电极选择要计算的频带，所选择的频率不一定要相同
对每一个时间点，计算一次所有试次间的相关系数，这样可以得到相关系数随时间变化的时间序列
如果选取多个频率，可以绘制出相关系数的 time-frequency map

3. 方法三

以一个电极作为“seed electrode”，同时选取一个 “seed time-frequency window”
对其他电极、时频区间，计算它们与seed electrode的相关系数。由此可以得到一个相关系数的 time-frequency-electrode map

Partial Correlations

保持Z不变，计算X和Y之间的偏相关系数，可以消除Z的影响：

$r_{xy\cdot z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{1-r_{xz}^2}\sqrt{1-r_{yz}^2}}$

用于消除体积传导效应的影响：如果X和Y是两个相距几厘米（比较远）的电极，而X和Z是相邻的电极。如果X和Y之间的相关性与Z和Y之间的相关性非常相似，那么X和Z之间可能存在体积传导，可以通过计算偏相关系数消除

Matlab技巧

进行时频分解后，可以先降采样，再计算相关系数
如果数据中没有特殊的值，可以自编代码计算Speaman相关系数，耗时比corr和corrcoef更短。在没有数值相同的数据的情况下，可以用下面的公式计算Spearman相关系数
$r=1-\frac{6\sum^n_{t=1}(x_t-y_t)^2}{n(n^2-1)}$
其中，x、y是两组功率数据，t是trial或time，n是trial或time的数目。

如果对计算速度有更高的要求，可以用最小二乘拟合。

28 | Granger Prediction

概述

Results from Granger causality analyses neither establish nor require causality.
Granger Prediction讨论的问题是：如果你知道电极B在过往时间内的活动，那么是否能够预测电极A在未来时间的活动？由此预测出的结果是否会比在只知道电极A在过往时间内活动的条件下预测出的结果更好？如果有统计数据支持“是”，那么可以说B对A存在着Granger预测（Granger因果）效应。
在进行Granger prediction前不应该降采样，采样率在250-1000Hz会比较合适

Univariate Autoregression | 单变量自回归

k阶单变量自回归AR(k)：用一个变量的时间数列作为因变量数列，用同一变量向过去推移k个时间步长的时间数列作自变量数列

$X_t=\sum^k_{n=1}a_nX_{t-n}+e_{xt}$

a是自回归系数，e是每个时间点的误差项
自回归模型假设时间序列是平稳的（Stationary），即统计特性不随时间改变，这也是使用Granger Prediction的条件

Bivariate Autoregression | 双变量自回归

$X_t=\sum^k_{n-1}a_nX_{t-n}+\sum^k_{n=1}b_nY_{t-n}+e_{xyt}$ $Y_t=\sum^k_{n-1}c_nY_{t-n}+\sum^k_{n=1}d_nX_{t-n}+e_{yxt}$

a、b、c、d是自回归系数，e是拟合误差，如果Y对X的预测值没有影响，即$X_t$公式中不包含Y，那么$e_{xyt}=e_{xt}$
Matlab从数据中提取自回归系数可以通过 BSMART Toolbox 中的armorf.m函数

Autoregression Errors and Error Variances

误差e越小，说明回归模型的拟合效果越好。误差的大小可以用误差的方差来衡量。
GrangerPrediction的数学定义（从y到x）：
$GrangerPrediction=\ln(\frac{var(e_x)}{var(e_{xy})})$
GrangerPrediction通常是正的，因为多变量自回归的拟合效果通常比单变量自回归的拟合效果更好，如果计算出的GrangerPrediction小于零，需要检查一下模型是否合适、数据是否违反了平稳性。

GrangerPrediction越大，$e_{xy}$越小，可以认为x和y之间的Connectivity越强。

Granger Prediction over Time

代码实现：

% load sample EEG data
load sampleEEGdata

% define channels for granger prediction
chan1name = 'o1';
chan2name = 'f5';

% Granger prediction parameters
% 时间窗口的长度
timewin = 200; % in ms
% 自回归拟合阶数（单位是ms）
order   =  27; % in ms

% temporal down-sample results (but not data!)
% 对结果进行降采样（在计算完GrangerPrediction之后）
times2save = -400:20:1000; % in ms


% convert parameters to indices
timewin_points = round(timewin/(1000/EEG.srate));
% 把阶数从ms转化为采样点数
order_points   = round(order/(1000/EEG.srate));

% find the index of those channels
chan1 = find(strcmpi(chan1name,{EEG.chanlocs.labels}));
chan2 = find(strcmpi(chan2name,{EEG.chanlocs.labels}));

% 为提高平稳性，需要减去ERP
% remove ERP from selected electrodes to improve stationarity
eegdata = bsxfun(@minus,EEG.data([chan1 chan2],:,:),mean(EEG.data([chan1 chan2],:,:),3));


% convert requested times to indices
times2saveidx = dsearchn(EEG.times',times2save');

% initialize
% x2y和y2x都是 1×length(times2save) 的零矩阵
[x2y,y2x] = deal(zeros(1,length(times2save))); % the function deal assigns inputs to all outputs
bic = zeros(length(times2save),15); % Bayes info criteria (hard-coded to order=15)

for timei=1:length(times2save)

    % data from all trials in this time window 提取timewindow内数据（在这里没有降采样）
    tempdata = squeeze(eegdata(:,times2saveidx(timei)-floor(timewin_points/2):times2saveidx(timei)+floor(timewin_points/2)-mod(timewin_points+1,2),:));

    % detrend and zscore all data
    for triali=1:size(tempdata,3)   % size(tempdata,3)就是EEG.trials
        % detrend：去趋势，去除低频漂移。zscore：使数据均值为0，方差为1
        tempdata(1,:,triali) = zscore(detrend(squeeze(tempdata(1,:,triali))));
        tempdata(2,:,triali) = zscore(detrend(squeeze(tempdata(2,:,triali))));

        % At this point with real data, you should check for stationarity
        % and possibly discard or mark data epochs that are extreme stationary violations.
    end

    % reshape tempdata for armorf 把所有trials的数据拼接成一行
    tempdata = reshape(tempdata,2,timewin_points*EEG.trials);

    % fit AR models (model estimation from bsmart toolbox)
    % 计算误差e
    [Ax,Ex] = armorf(tempdata(1,:),EEG.trials,timewin_points,order_points);
    [Ay,Ey] = armorf(tempdata(2,:),EEG.trials,timewin_points,order_points);
    [Axy,E] = armorf(tempdata     ,EEG.trials,timewin_points,order_points);

    % time-domain causal estimate
    % 计算GrangerPrediction
    y2x(timei)=log(Ex/E(1,1));
    x2y(timei)=log(Ey/E(2,2));

    % test BIC for optimal model order at each time point
    % (this code is used for the following cell)
    for bici=1:size(bic,2)
        % run model
        [Axy,E] = armorf(tempdata,EEG.trials,timewin_points,bici);
        % compute Bayes Information Criteria
        bic(timei,bici) = log(det(E)) + (log(length(tempdata))*bici*2^2)/length(tempdata);
    end
end

% draw lines
figure
plot(times2save,x2y)
hold on
plot(times2save,y2x,'r')
legend({[ 'GP: ' chan1name ' -> ' chan2name ];[ 'GP: ' chan2name ' -> ' chan1name ]})
title([ 'Window length: ' num2str(timewin) ' ms, order: ' num2str(order) ' ms' ])
xlabel('Time (ms)')
ylabel('Granger prediction estimate')

Model Order

可以通过计算Bayes information criterion（BIC）来确定自回归模型的阶数：

$BIC = \ln{(\det{E})}+(2^2m\ln n)n^{-1}$

E是双变量误差矩阵，2是电极数目，m是回归模型阶数，n是时间点数目。

for bici=1:size(bic,2)	% bici是回归模型阶数值，
，对不同的阶数值，分别计算
        % run model
        [Axy,E] = armorf(tempdata,EEG.trials,timewin_points,bici);
        % compute Bayes Information Criteria
        bic(timei,bici) = log(det(E)) + (log(length(tempdata))*bici*2^2)/length(tempdata);
    end

BIC的值越小越好，但在不同的时间点BIC最小值所对应的阶数可能会不同，因此很难找出一个最优的阶数。

Frequency Domain Granger Prediction

计算Frequency domain Granger Prediction时，不能先滤波再计算GrangerPrediction。具体代码实现：

min_freq = 10; % in Hz, using minimum of 10 Hz because of 200-ms window
max_freq = 40;

order_points = 15;	% 自回归模型阶数

frequencies = logspace(log10(min_freq),log10(max_freq),15);

% initialize：2代表 电极1→电极2、电极2→电极1 两个方向的结果
tf_granger=zeros(2,length(frequencies),length(times2save));


for timei=1:length(times2save)

    % data from all trials in this time window
    % (note that the ERP-subtracted data are used)
    % eegdata中只保留了两个电极的数据，需要减去ERP
    tempdata = squeeze(eegdata(:,times2saveidx(timei)-floor(timewin_points/2):times2saveidx(timei)+floor(timewin_points/2)-mod(timewin_points+1,2),:));

    % detrend and zscore all data
    for triali=1:size(tempdata,3)
        tempdata(1,:,triali) = zscore(detrend(squeeze(tempdata(1,:,triali))));
        tempdata(2,:,triali) = zscore(detrend(squeeze(tempdata(2,:,triali))));
    end

    % reshape tempdata for armorf
    tempdata = reshape(tempdata,2,timewin_points*EEG.trials);

    % fit AR models
    [Ax,Ex] = armorf(tempdata(1,:),EEG.trials,timewin_points,order_points);
    [Ay,Ey] = armorf(tempdata(2,:),EEG.trials,timewin_points,order_points);
    [Axy,E] = armorf(tempdata     ,EEG.trials,timewin_points,order_points);

    % code below is adapted from bsmart toolbox function pwcausal.m
    % corrected covariance
    eyx = E(2,2) - E(1,2)^2/E(1,1);
    exy = E(1,1) - E(2,1)^2/E(2,2);
    N = size(E,1);

    for fi=1:length(frequencies)

        % transfer matrix (note the similarity to Fourier transform) 
        % 不理解这样做的原因
        H = eye(N);
        for m = 1:order_points
            H = H + Axy(:,(m-1)*N+1:m*N)*exp(-1i*m*2*pi*frequencies(fi)/EEG.srate);
        end

        Hi = inv(H);
        S  = H\E*Hi'/EEG.srate;

        % granger prediction per frequency
        tf_granger(1,fi,timei) = log( abs(S(2,2))/abs(S(2,2)-(Hi(2,1)*exy*conj(Hi(2,1)))/EEG.srate) );
        tf_granger(2,fi,timei) = log( abs(S(1,1))/abs(S(1,1)-(Hi(1,2)*eyx*conj(Hi(1,2)))/EEG.srate) );
    end
end % end time loop

自回归模型的阶数过小（小于奈奎斯特频率）会影响Granger Prediction的频率精度

Time Series Covariance Stationarity

Stationarity is a statistical term that refers to a time series having the same statistical properties over time.
Stationarity is an assumption of autoregression model estimation.
Methods to make data stationary
- Detrending and z-normalization (subtract the mean and divide by the standard deviation)
- Using shorter time segments
- Subtracting the ERP from single trials (non-phase-locked)
- Apply Granger prediction to the derivative of the time series, that is, the difference between activity at each time point and the previous time point.
评估数据的平稳性：可以用 The Granger Causal Connectivity Analysis toolbox 中的函数cca_kpss和cca_check_cov_stat

Baseline Normalization of Granger Prediction Results

两种baseline normalization方法：
- 最终结果减去baseline
- 转化为相对于baselined的百分比：100*(x2y-mean(x2y(baseidx(1):baseidx(2))))/mean(x2y(baseidx(1):baseidx(2)))
The percentage change transform facilitated an interpretation of the patterns of the connectivity that are specifically task related.

29 | Mutual Information | 互信息

Mutual information is a simple but robust framework for quantifying the amount of shared information between two variables.

Entropy ( Shannon entropy, 信息熵)

Shannon entropy 指一个变量包含的信息量

1. 计算一段连续数据的entropy

$H(X)=-\sum^n_{i=1}p(x_i)\log_2p(x_i)$

在数据的最小值和最大值之间划分n个bin，每个bin内装着符合一定范围的数据，$p(x_i)$代表第i个bin中数据个数占总数据的百分比，H即为entropy的度量。

% number of bin numbers
nbins = 10;

% bin data, transform to probability, and eliminate zeros
hdat = hist(signal1,nbins(nbini));
hdat = hdat./sum(hdat);
    
% compute entropy
% eps是matlab中的最小数值分辨率，用来防止出现1og(0)的情况
entropyByBinSize = -sum(hdat.*log2(hdat+eps));

可以看出，entropy与数据的时间排列无关，只与数据的值的分布有关

2. 确定bin的数目

Freedman-Diaconis rule：
$nbins = \lceil \frac{\max(x)-\min(x)}{2Q_xn^{-1/3}}\rceil$
其中$Q_x$是数据的四分位数范围（将数据从小到大排列，用排在75%的数据减去排在25%的数据），n是数据点数目
Scott ’ s rule：

用3.5s代替Freedman-Diaconis rule里的2Q，其中s指的是数据的标准差（数据需要正态分布）
Sturges ’ s rule：
$nbins=1+\log_2n$

fd_bins      = ceil(maxmin_range/(2.0*iqr(signal1)*n^(-1/3))); % Freedman-Diaconis 
scott_bins   = ceil(maxmin_range/(3.5*std(signal1)*n^(-1/3))); % Scott
sturges_bins = ceil(1+log2(n)); % Sturges

对同一组分析，nbins的值要保持一致，如果有多个变量，可以分别计算合适的nbins值，最后取平均值作为所有变量的nbins

3. 对Entropy的理解

熵是对不确定性的一种度量方法。更高的熵表明该系统可以具有更多的状态或取值。
entropy可以over time也可以over trial计算，而且因为它不受时间排列的影响，所以也可以把所有time和trial的数据合成一组数据计算。

4. Joint Entropy | 联合熵

$H(X,Y)=-\sum^m_{j=1}\sum^n_{i=1}p(x_i,y_y)\log_2p(x_i,y_i)$

$p(x_i,y_i)$是在 $signal_1$ 中落在第$x_i$个 bin 且在 $signal_2$ 中落在第 $y_2$ 个 bin 的点的概率（看下面的代码会比较好理解）

% 分别计算每组数据需要的bins的数目，最后取平均值作为使用的bins数目
% determine the optimal number of bins for each variable
n            = length(signal1);
maxmin_range = max(signal1)-min(signal1);
fd_bins1     = ceil(maxmin_range/(2.0*iqr(signal1)*n^(-1/3))); % Freedman-Diaconis 

n            = length(signal2);
maxmin_range = max(signal2)-min(signal2);
fd_bins2     = ceil(maxmin_range/(2.0*iqr(signal2)*n^(-1/3))); % Freedman-Diaconis 

% 取均值
% and use the average...
fd_bins = ceil((fd_bins1+fd_bins2)/2);

% 将 signal1 和 signal2 分箱。每个信号的数值范围会被分成 fd_bins 个区间（bin）
% [bincounts,ind] = histc(x,binranges), ind存储的是每个index上的数据被放在了哪一个bin里
% bin data (using histc this time)
edges = linspace(min(signal1),max(signal1),fd_bins+1);
[nPerBin1,bins1] = histc(signal1,edges);

edges = linspace(min(signal2),max(signal2),fd_bins+1);
[nPerBin2,bins2] = histc(signal2,edges);

% compute joint frequency table
jointprobs = zeros(fd_bins);
for i1=1:fd_bins
    for i2=1:fd_bins
        % 计算在 signal1 中落在第 i1 个 bin 且在 signal2 中*对应位置的点*落在第 i2 个 bin 的点的数量
        % 注意与 sum(bins1==i1)+sum(bins2==i2) 不同
        % bins1==i1 和 bins2==i2 分别是两组布尔向量1和2，bins1==i1 & bins2==i2是布尔向量3，
        % 当1和2中对应位置的元素都为1时，3中对应位置的元素才是1
        jointprobs(i1,i2) = sum(bins1==i1 & bins2==i2);
    end
end
% 进行归一化，使联合频率表中的值变为概率，整个矩阵的总和为 1
jointprobs=jointprobs./sum(jointprobs(:));

Mutual Information

1. 计算公式

$MI(X,Y)=H(X)+H(Y)-H(X,Y)$

mutual information 不能区分线性和非线性、正相关和负相关等两个变量形状之间的关系

2. 所需数据点的数目

数据点数目越少，对entropy和mutual information的计算值就越偏大：

$\Delta H=\frac{bins-1}{2Nln2}$ $\Delta MI=\frac{(bins-1)^2}{2N\ln2}$

Lagged Mutual Information

把一组数据相对于另一组数据进行时移，这样计算出的互信息可以反映有向的功能连接

30 | Cross-Frequency Coupling

Cross-frequency coupling analyses require both the high temopral resolution and temporal precision.

A Priori Phase-Amplitude Coupling (PAC)

the phase of one frequency band ⬌ the power of another frequency band (typically higher)

区分：

a priori phase-amplitude coupling：在先验假设的前提下，已经确定了要检验的两个频带
mixed a priori/exploratory phase-amplitude coupling ：已确定一个频带，对其他频带进行探索性分析
exploratory phase-amplitude coupling：两个频带都没有确定

PAC的计算：

和wITPC类似，只不过使用的weight（$a_t$）是某一频带的power（原始数据，未经baseline normalization），而欧拉公式中的phase（$\phi_t$）是另一个待分析频带的phase

$PAC=\left|n^{-1}\sum^n_{t=1}a_te^{i\phi_t}\right|$

obsPAC = abs(mean(pwr.*exp(1i*phase)));

$PAC_Z$

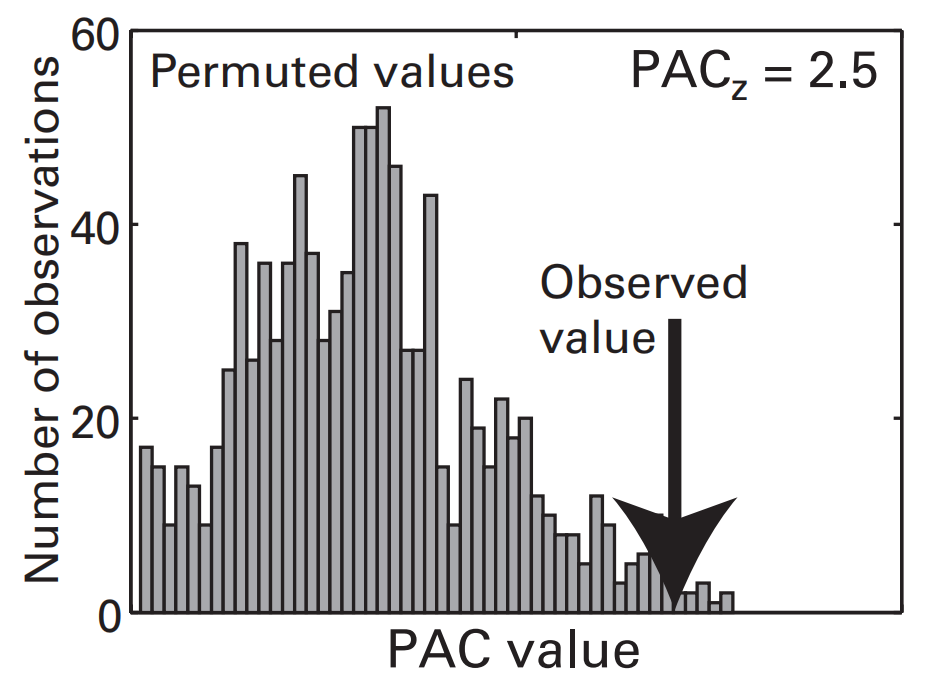
零假设下的PAC值分布：打乱power的时间顺序（随机置换），计算得一个PAC，重复多次，由此计算出的所有PAC的分布构成零假设下的PAC分布。
$PAC_Z$：将前面计算观测得到的一个PAC值减去零假设下PAC分布的平均值，再除以零假设下PAC分布的标准差，则可以得到$PAC_Z$
归一化后的PAC值（$PAC_Z$）不会受功率的大小影响，也不受离群值影响，且便于统计分析。

% 计算观测得到的一个PAC值
obsPAC = abs(mean(pwr.*exp(1i*phase)));
% 随机置换的次数
num_iter = 1000;
% 每随机置换一次，计算得到的PAC值
permutedPAC = zeros(1,num_iter);

for i=1:num_iter
    
    % select random time point
    random_timepoint = randsample(round(length(eeg)*.8),1)+round(length(eeg)*.1);
    
    % shuffle power
    timeshiftedpwr = [ pwr(random_timepoint:end) pwr(1:random_timepoint-1) ];
    
    % compute PAC
    permutedPAC(i) = abs(mean(timeshiftedpwr.*exp(1i*phase)));
end

% compute PACz
pacz = (obsPAC-mean(permutedPAC))/std(permutedPAC);

随机置换时间顺序的方法：

在某个随机时间点截断数据，交换两段数据

% Permutation method 1: select random time point
random_timepoint = randsample(round(length(eeg)*.8),1)+round(length(eeg)*.1);
timeshiftedpwr   = [ pwr(random_timepoint:end) pwr(1:random_timepoint-1) ];
permutedPAC = abs(mean(timeshiftedpwr.*exp(1i*phase)));

（不推荐）直接打乱时间

% Permutation method 2: totally randomize power time series
permutedPAC = abs(mean(pwr(randperm(length(pwr))).*exp(1i*phase)));

先对数据进行FFT，打乱FFT后所得数据的相位，再ifft

% Permutation method 3: FFT-based power time series randomization
f = fft(pwr); % compute FFT
A = abs(f);   % extract amplitudes
zphs=cos(angle(f))+1i*sin(angle(f)); % extract phases
   powernew=real(ifft(A.*zphs(randperm(length(zphs))))); % recombine using randomized phases (note: use original phases to prove that this method reconstructs the original signal)
powernew=powernew-min(powernew);
    
permutedPAC = abs(mean(powernew.*exp(1i*phase)));

指的是当我们发现某频带的幅值和另一频带的相位存在幅相耦合时，我们应该如何判断它们之间究竟是真的存在耦合关系，还是它们独立地对刺激等任务作出了相同的time-locked响应。

当phase是time-locked时，相应的ITPC值应当较大。因此，我们应该尽可能避免在ITPC值较大的时间段内使用PAC，也可以从数据中减去ERP，去除相位锁定的成分，再计算PAC

Mixed A Priori/Exploratory Phase-Amplitude Coupling

已确定一个频率，对其他频率进行探索性分析，即在 lower frequency for phase 和 upper frequency for power 中，选一个作为 priori band，另一个则为 exploratory band to find that the strongest coupling with the other frequency can be observed.

所以可以固定一个频率，遍历另一频率，对每一种组合计算一次$PAC_Z$，找到使$PAC_Z$最大的频率组合。但是找到这一对频率后，再对这两个频率计算出的PAC值使用p-value去解释其显著性就不太合适了，因为在这里我们已经发现它们在所有频率组合中是相关性最强的。

Exploratory Phase-Amplitude Coupling

两个频率都没有确定，对每一对频率组合都计算一次$PAC_Z$，计算量较大

31 | Graph Theory

Networks as Matrices and Graphs

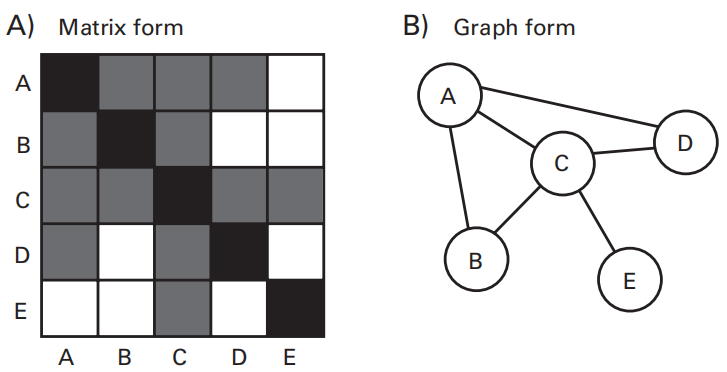
An EEG all-to-all connectivity matrix, is one slice of a 5-D hypercube (electrodes - electrodes - time - frequency - condition)

Thresholding Connectivity Matrices

choose a threshold value
threshold value 以上的设为1（或保留原值），以下的设为0

常用的 threshold value 选择方法：

比connectivity的中值高一个标准差
保留前k个最大的connectivity

Connectivity Degree

Connectivity Degree 反映了某一电极作为“枢纽”的程度
计算方法：对某一电极，除自己以外的所有大于threshold value的connectivity数目。最后可以将结果除以“电极数目减一”，转化为百分比。
最终所得结果是一个 1×electrodes 的数值矩阵，可以用topographical map表示

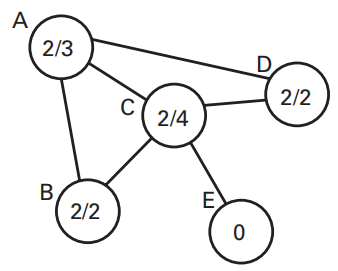
Clustering Coefficient | 聚集系数

Clustering Coefficient 指的是在所有与电极A的connectivity大于threshold的电极中，有多少电极它们彼此之间的connectivity也在阈值之上。（你的朋友中有多少人彼此之间也同样是朋友）
计算公式
$clustcoef_i=\frac{\sum_{k=1}^{n}\sum_{j=k}^n v_{ij}}{n_i}$
其中，i是电极，k,j是与i的connectivity大于阈值的电极，如果电极k和j之间的connectivity大于阈值，则$v_{ij}$是1，否则是0，因此分子即为包含电极i的三角形数目。分母$n_i$是电极 i 的Connectivity degree。如果degree为1，则cluster coefficient为0

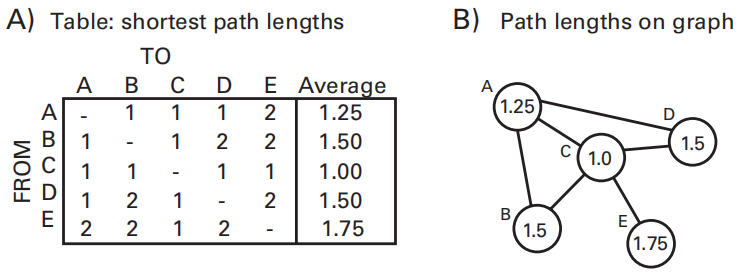
Path Length | 平均路径长度

Path Length 是某个电极（node）到其他电极的平均距离

Small-World Networks | 小世界网络

Collective dynamics of ‘small-world’ networks | Nature

Small-World Networks: high clustering coeffecience and low path length. When rewiring (transition from regular to random), path length drops faster than clustering coefficient.

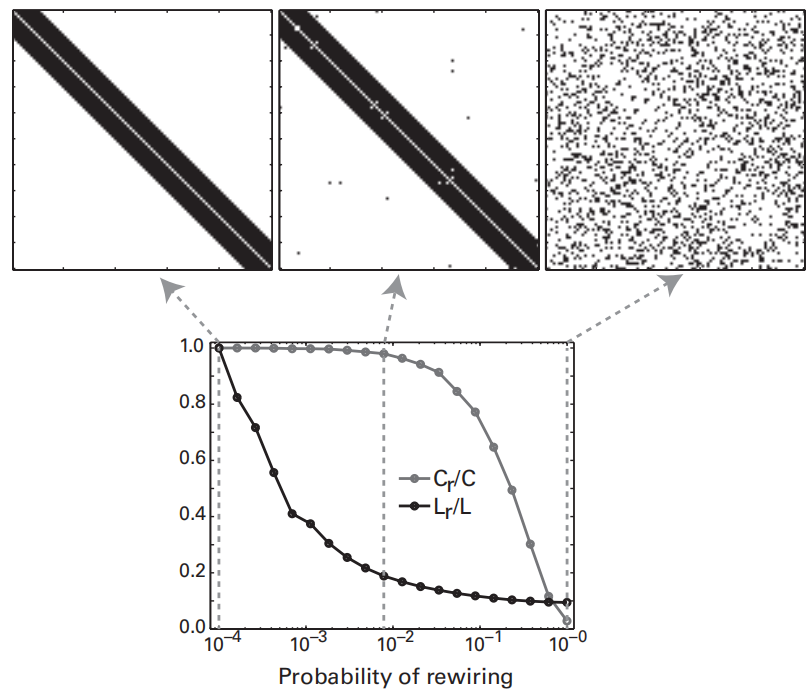
判断是否为Small-World Networks：

$swn=\frac{C/C_r}{L/L_r}$

分子分母分别是 当前图和random图(Erdős-Rényi random graphs)的平均clustering coefficient / path length比值。如果swn大于1，可以认为当前网络具有小世界网络的特征。

32 | Advantages and Limitations of Different Statistical Procedures

Level: the unit of data

Within subject statistics (level-1): consider the trial to be the unit for analysis. Recommended when having many trials from a small number of subjects.
Group-level statistics (level-2): consider the subject to be the unit for analysis

P-Value

通常情况下，p-Value<0.05可以被认为是显著的
p-Value的最后一位小数通常是5或1，如果p=0.323会比较奇怪
对hypothesis-driven rearch，对p值的要求没那么严格，通常p=0.05就足够了，但对于exploratory analyses，需要对p值进行更严格的设置，或者结合multiple-comparisons corrections使用
p-Value的缺点：based on the number of data points，如果data points足够，很小的effects也可以有很小的p-value，反之，如果数据点少，即使effects很大，p-Value也可能很大

Multiple-Comparisons Corrections | 多重比较

Bonferroni correction: assumes that the tests are independent of each other, and corrects for the number of tests, not the amount of information available in those tests.
nonparametric permutation testing provides an appropriate control for multiple comparisons.

Type I and Type II Errors

1. 定义

第一类错误（Type I Error）和第二类错误（Type II Error）是统计学中的两种常见错误类型，通常出现在假设检验的过程中。

第一类错误（Type I Error）：也称为假阳性错误，是指错误地拒绝了原假设（即 ( $H_0$ ) ），也就是说，实际原假设是真实的，但我们在统计检验中认为它是假的。第一类错误的概率通常用 ( $\alpha$ ) （显著性水平）来表示。
第二类错误（Type II Error）：也称为假阴性错误，是指错误地接受了原假设，也就是说，实际原假设是假的，但我们在统计检验中没有拒绝它。第二类错误的概率通常用 ( $\beta$ ) 来表示，1-$\beta$ 称为检验的统计功效（Power）。

2. 总结

第一类错误：你认为有新发现（拒绝了原假设），但实际上没有（即原假设是真实的）。
第二类错误：你认为没有新发现（接受了原假设），但实际上有（即原假设是假的）。

3. 图示

实际情况 \ 检验结果	拒绝 ( $H_0$ ) （认为有新发现）	接受 ($ H_0$ ) （认为无新发现）
( $H_0$ ) 真	第一类错误	正确决定
( $H_0$ ) 假	正确决定	第二类错误

4. 例子

假设你在不同的脑区测量α波段功率，比较安静状态和任务状态下的某个特定频段的EEG功率差异。

第一类错误：你发现两种状态下的α波功率存在显著差异，但实际上这是由于噪声或偶然性引起的，这两个条件实际上没有差异。
第二类错误：实际情况下，安静状态下的α波功率显著高于任务状态，但由于数据的噪声、实验设计或其他因素，你没有检测到这个差异，得出两者功率相同的结论。

5. 两种错误发生概率的关系

$\alpha$ 和 $\beta$ 的关系：如上图中灰色虚线（$\alpha$ threshold）所示，$\alpha$ 增大， $\beta$ 就会相应减小。
对于exploratory的研究，我们希望第一类错误发生的概率$\alpha$小一些；对于 hypothesis-driven的研究，我们希望第二类错误发生的概率$\beta$小一些

如何选择统计方法

parametric statistics: assuming that data were drawn from a known distribution (like Gaussian distribution)
nonparametric statistics: no assumption is made about the population distribution from which the data were drawn. Often use permutation testing.
如果数据不是正态分布的，而又需要使用参数统计，可以先对数据进行处理，比如对于时频数据，进行baseline correction，对于PAC，进行permutation testing

33 | Nonparametric Permutation Testing 非参数置换检验

Creating a Null-Hypothesis Distribution

离散条件下的零假设：
- 情景：有两种离散的condition（A和B），要验证的假说是A条件下的EEG activity比B大。
- 零假设：两种条件下的EEG没有差别。即，如果我把每一个数据点随机地看作是条件A或条件B下的（也可以随机地交换条件A和B下的数据），所使用的检验统计量也不会发生改变。
连续条件下的零假设
- 如果A和B是两个连续的变量，在零假设下，保持一个变量A不变，改变另一个变量B，检验统计量（如相关系数）不会发生改变

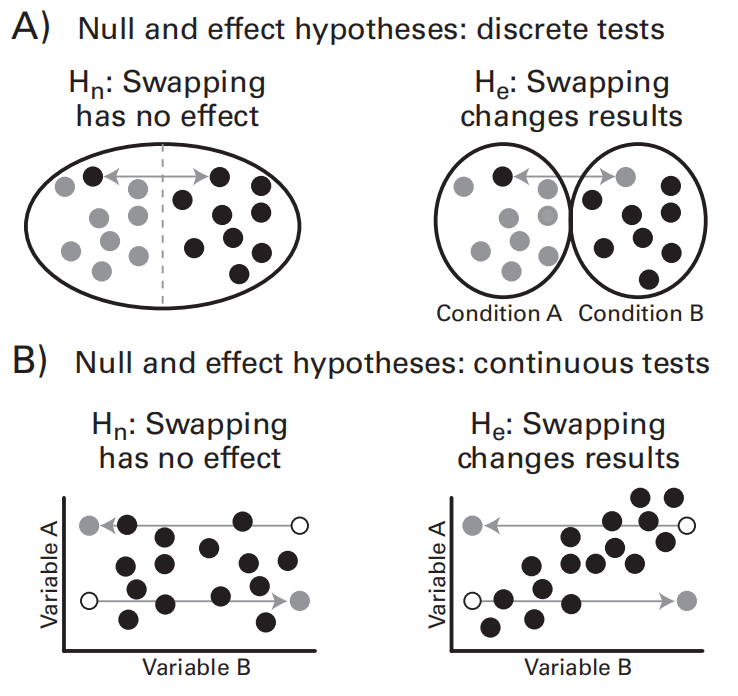
重复上面的随机置换步骤，每置换一次可以计算出一个统计检验量，最终就可以得到在零假设下检验统计量的分布。
将我们在实验中观测得的检验统计量与零假设下的检验统计量分布相比较
- 如果在零假设的分布内，不能拒绝原假设
- 如果far enough away from the null-hypothesis distribution，即在零假设下几乎不可能发生，那么可以拒绝原假设，即认为两种条件下的被检验量存在显著的差异。

Determining Statistical Significance

p值的计算（两种方法）
- 在零假设下所有比所观测到的检验统计量更极端的数据之和除以 零假设下的总数据
  $p-Value=\frac{n_{v>v_e}}{n}$
- 先将观测到的统计量转化为Z value
  $Z=\frac{v_e-\overline{V_n}}{std(V_n)}$
  然后再根据其在Gaussian分布中的位置计算p值

Multiple Comparisons | 多重比较

多重比较 | 多元统计分析讲义 (pku.edu.cn)

1. 所讨论的问题

多次进行检验，如果每次检验的第一类错误概率是$\alpha$，各次检验独立，则检验$m$次，在所有零假设都成立的情况下至少犯一次第一类错误的概率为

$1-(1-\alpha)^m$

可以发现，检验的次数越多（m越大），犯第一类错误的概率越大。如何避免这种问题？

2. Bonferroni correction

Divide the p-value threshold by the number of tests that will be evaluated.
If you have three statistical tests, the p-value significance threshold per test is 0.05/3=0.016667

3. correcting for multiple comparisons within the framework of nonparametric permutation testing

修正前：每个时频点有自己的统计值，基于这些值在每个时频点下生成原假设分布
修正后：基于整个时频图生成原假设分布

4. Pixel-based multiple-comparisons correction

步骤

对每个时频点进行置换检验，计算p值，把整个时频图遍历一遍后，保留绝对值最大（最极端）的p值（如果是双侧检验，需保留最大和最小值）
重复上面的计算，得到一组最大/最小p值分布
对于双侧检验，以2.5%和97.5%处的p值作为阈值；对于单侧检验，以5%或95%处的p值作为阈值

5. Corrections for Multiple Comparisons Using Cluster-Based Statistics

Because of autocorrelation in the data, a finding is significant if it is “ big enough, ” that is, if enough neighboring pixels also have suprathreshold values. Individual pixels that are significant are therefore considered false alarms. 单个、没有聚集的显著时频点可能是有问题的
步骤
- 每个时频点生成一个零假设分布
- threshold每个时频点的检验统计量（该threshold需自己设置，称为precluster threshold），生成一张map
- 识别map中的cluster，可以用Matlab函数bwlabeln或bwconncomp
- 选择指标（聚集点数目和统计参数之和，或其他）最大的一个cluster，保存该指标
- 重复上述步骤，得到指标的一组分布，以分布的95%位置处的值作为cluster threshold

34 | Within-Subject Statistical Analyses