Untitled

一、控制系统介绍

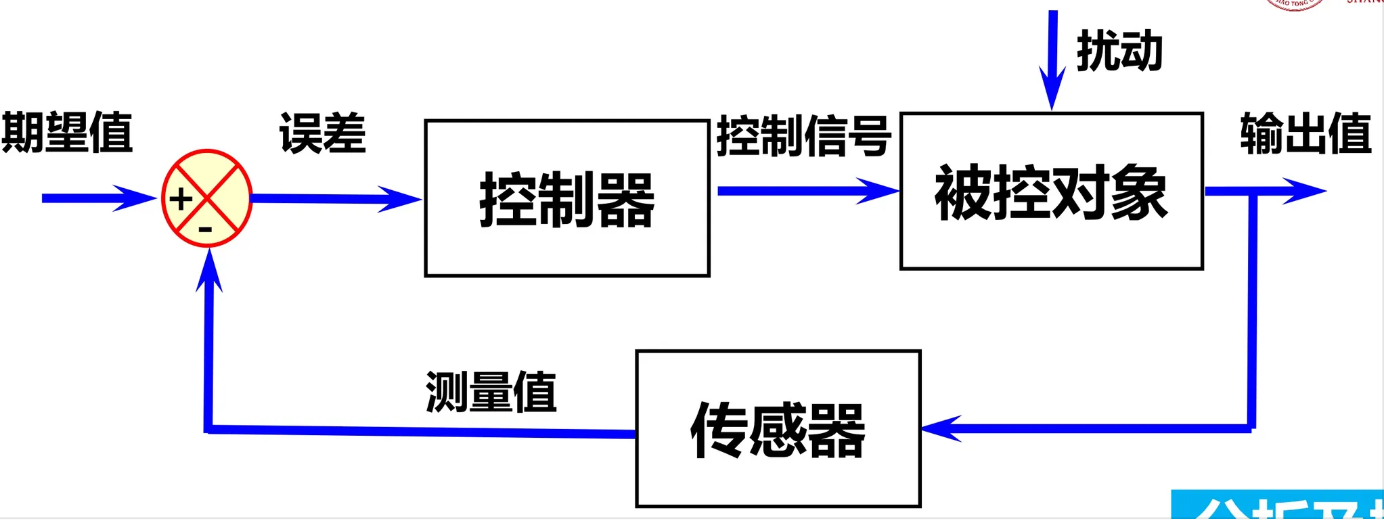
image-20241015093406434

  • 闭环控制的主要特点：1. 检测偏差；2.根据偏差调整控制量，从而减小或消除偏差
  • 被控对象、被控变量、控制信号、过程、扰动、反馈控制
  • 开环控制的优缺点
  • 闭环控制的优缺点
  • 考点：判断某系统是否是反馈控制系统

二、Laplace变换

  • 会用公式就行

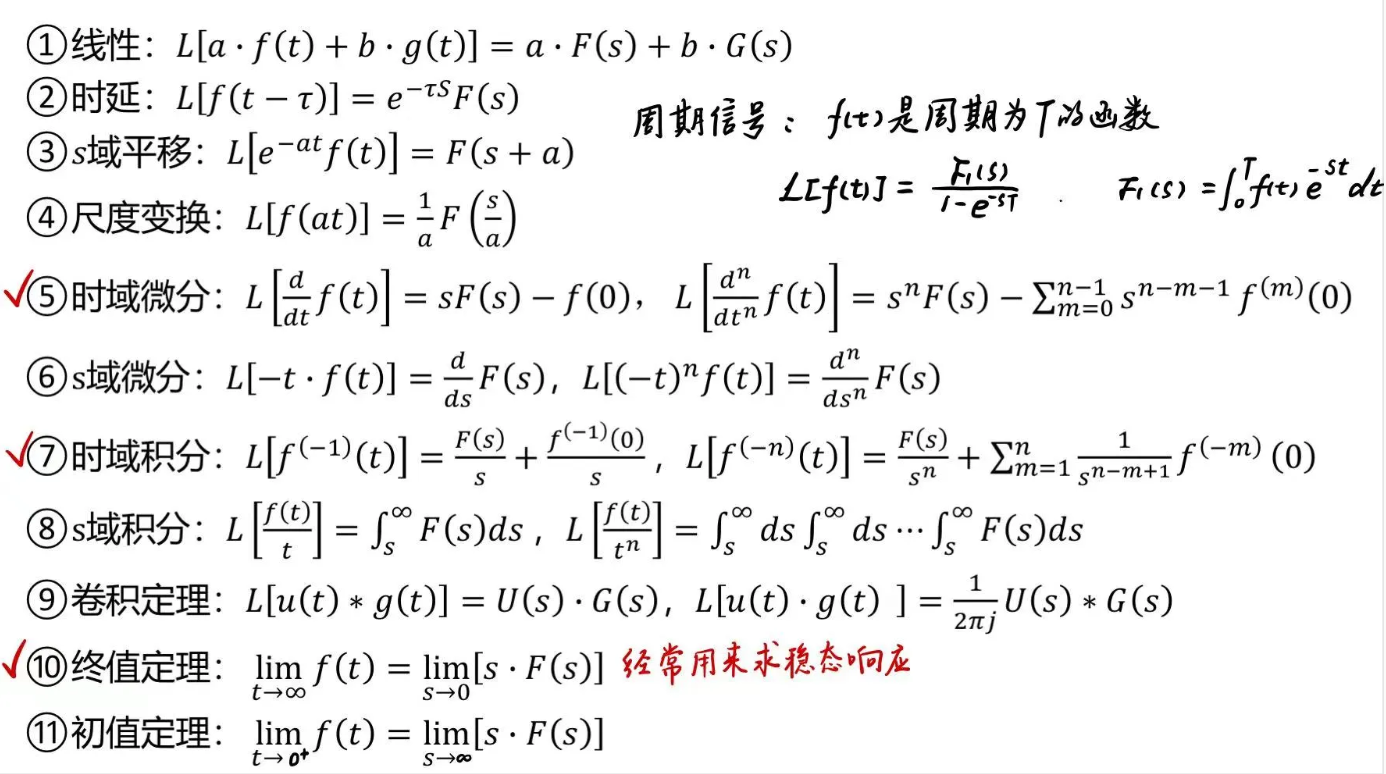
    image-20241015093455248

三、机械和电气系统建模

  • 质量-弹簧-阻尼系统

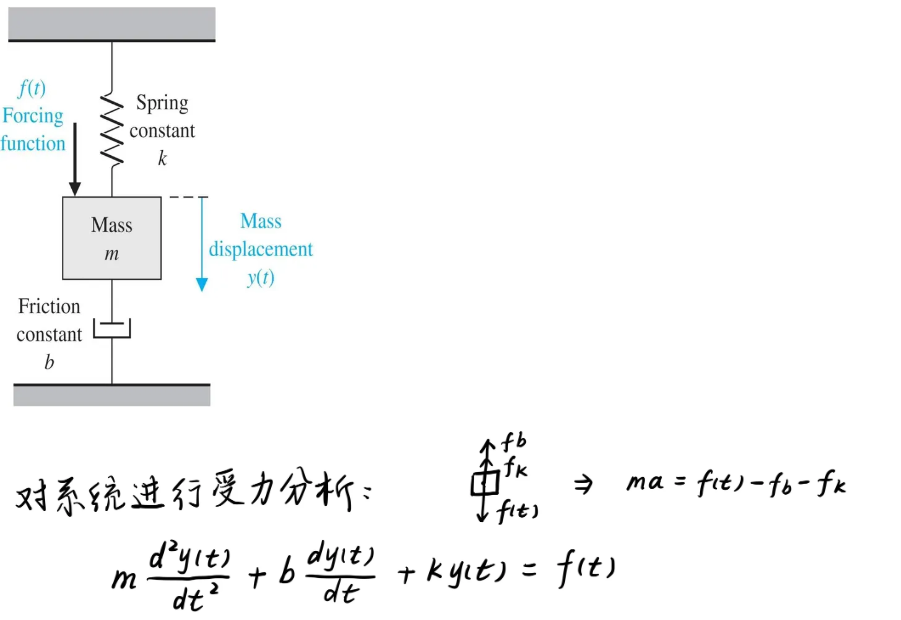
    image-20241015093523691

    • 为什么不考虑重力（没有mg项）：因为是以静止状态下的平衡工作点（无外部输入）作为零点，此时重力已经被弹簧的拉力平衡掉了

    • 其他的机械系统可以用同样的方法进行分析

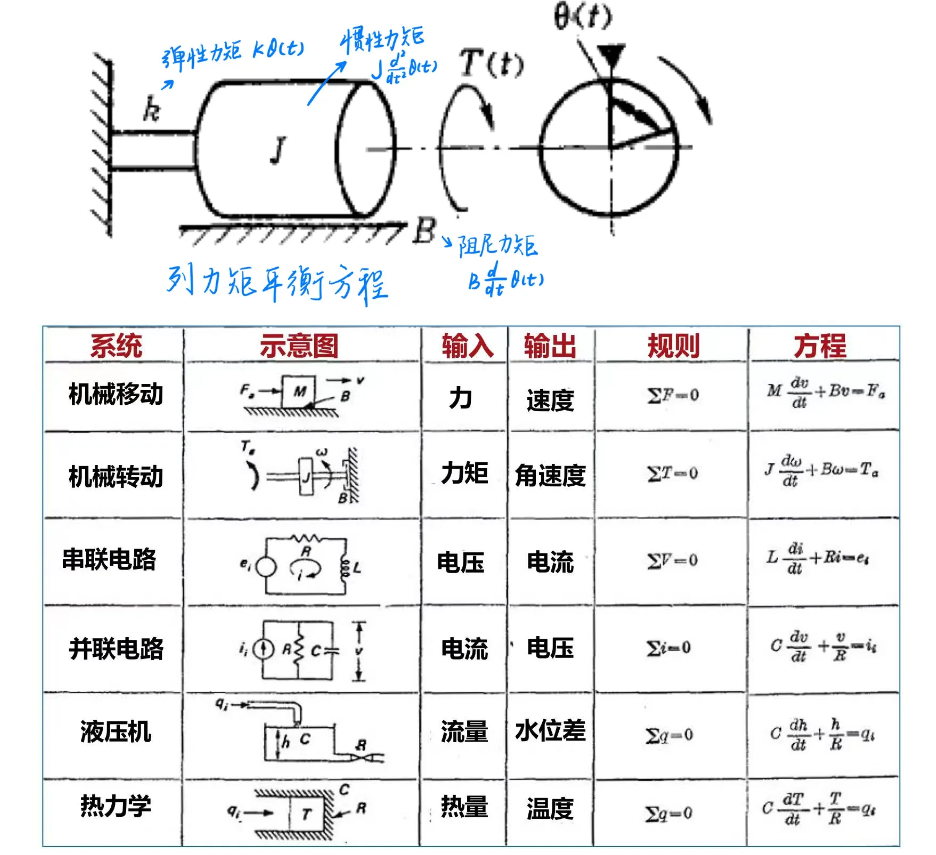
      image-20241015093615701

  • 机械传动系统：平动-转动系统、齿轮传动系统

  • 电气系统

    • 电阻：$u(t)=Ri(t)$

      电容：$u(t)=\frac{1}{C}\int i(t)dt$ 或 $i(t)=C\frac{\mathrm{d} u(t)}{\mathrm{d} t}$

      电感：$u(t)=\frac{1}{C}\frac{\mathrm{d} i(t)}{\mathrm{d} t}$

    • 列KCL、KVL方程求解

    • 复阻抗法：

      电阻：$Z=R$

      电容：$Z=\frac{1}{Cs}$

      电感：$Z=Ls$

    • 运放：虚短、虚断

    • 微分方程的阶数由独立储能元件个数决定

四、传递函数

  • 传递函数$G(s)$：线性定常系统、初值为0、单数单输出，输出的Laplace变换$Y(s)$与输入的Laplace变换$U(s)$的比值

  • 单位脉冲输入$δ(t)$，传递函数就是输出的Laplace变换：$G(s)=Y(s)$

  • 对输入求导，输出也会求相应的导数

    • 已知输入为单位斜坡响应$u(t)=t$时的输出$y(t)$，则传递函数为$y’’(t)$

    • 一阶系统：

      image-20241015093741538

  • 典型传递函数：

    • 比例/放大环节 $G(s)=K$
    • 积分环节 $G(s)=\frac{1}{s}$（若输入突然除去，积分停止，输出维持不变）
    • 微分环节 $G(s)=s$
    • 惯性环节 $G(s)=\frac{1}{Ts+1}$
    • 一阶微分环节 $G(s)=Ts+1$
    • 二阶振荡环节 $G(s)=\frac{1}{T^2s^2+2ζTs+1}$
    • 二阶微分环节 $G(s)=T^2s^2+2ζTs+1$
    • 延迟环节 $G(s)=e^{-\tau s}$

五、方框图

  • 方框图的简化

  • 简单版Mason公式：适用于有一条前向通路的系统

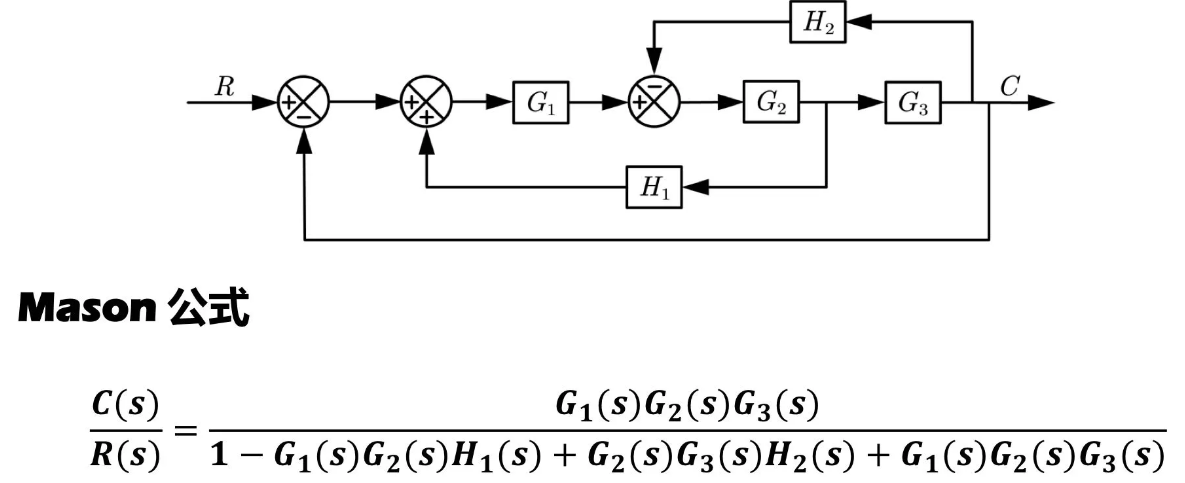
    image-20241015093913781

  • 几个定义

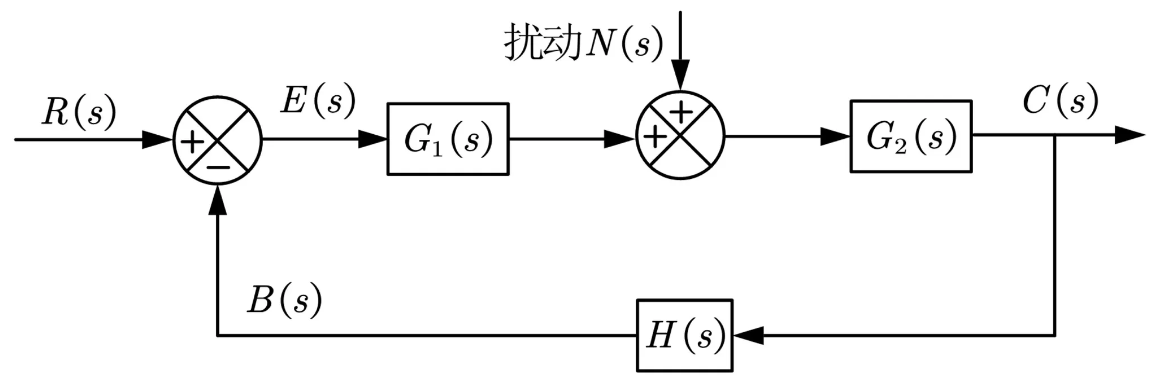
    image-20241015094132292

    • 前向通路：$R(s)$到$B(s)$

    • 反馈通路：$C(s)$到$B(s)$

    • 闭环传递函数：$\frac{C(s)}{R(s)}=\frac{G_1G_2}{1+G_1G_2H}$

    • 开环传递函数：反馈通路末端断开 $\frac{B(s)}{E(s)}=G_1G_2H$

    • 前向传递函数：$\frac{C(S)}{E(s)}=G_1G_2$

    • 误差传递函数

      ：以$E(s)$为输出，以$R(s)$或$N(s)$为输入的闭环传递函数

      • $\frac{E(s)}{R(s)}=\frac{1}{1+G_1G_2H}$ 与开环传递函数有关
      • $\frac{E(s)}{N(s)}=\frac{-G_2H}{1+G_1G_2H}$

  • 输入$R(s)$和扰动$N(s)$同时作用时的输出

    • 只考虑输入$R(s)$，则 $C(s)=\frac{G_1G_2}{1+G_1G_2H}R(s)$
    • 只考虑$N(s)$，则 $C(s)=\frac{G_2}{1+G_1G_2H}N(s)$
    • 同时考虑两者$C(s)=\frac{G_1G_2}{1+G_1G_2H}R(s)+\frac{G_2}{1+G_1G_2H}N(s)$

  • 可以发现系统的闭环传递函数（反馈通路没有断开）的分母均为$1+G_1G_2H$（系统的特征多项式），这说明

    • 不管外作用加在系统的哪一个位置（$R(s)$处还是$N(s)$处，或者其他位置），系统都有着相同的特征多项式，系统闭环传递函数都有着相同的极点，这是系统的一种固有特性

六、信号流图

  • 几个定义

    • 前向通路：从输入节点到输出节点，通过任一节点不多于一次的通路
    • 回路：起点和终点重回，通过任一节点不多于一次
    • 不接触回路：相互间没有任何公共节点的回路
    • 增益：所在路径上所有传播（传递函数）的乘积

  • 根据系统方程绘制信号流图

  • 根据方框图绘制信号流图

    • 节点的选取：一般取输入、输出、加法器后（支路汇总的地方）、出现分支的地方 作为节点

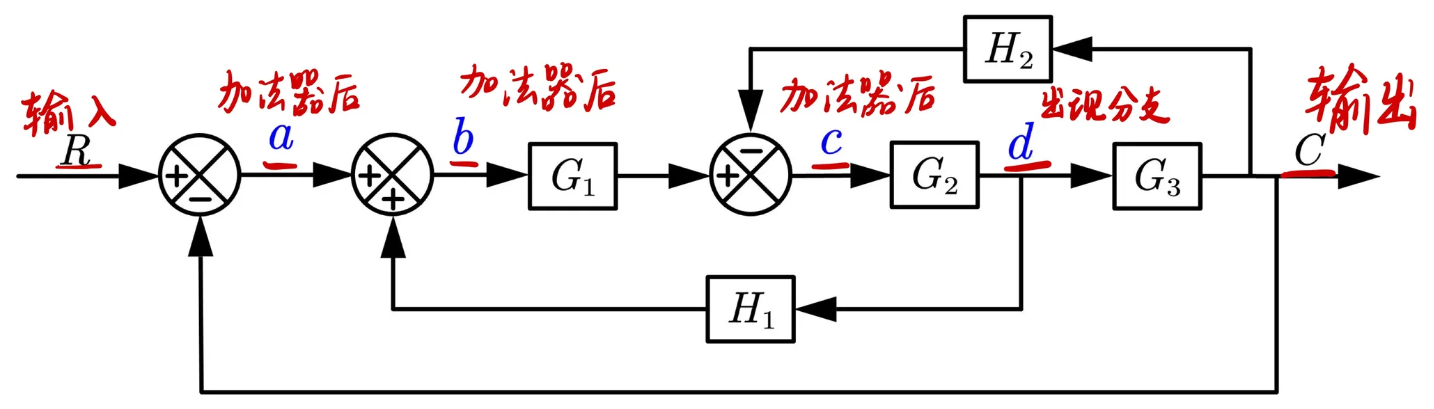
      image-20241015094231726

  • Mason公式：找对通路、回路后套公式

    image-20241015094304633

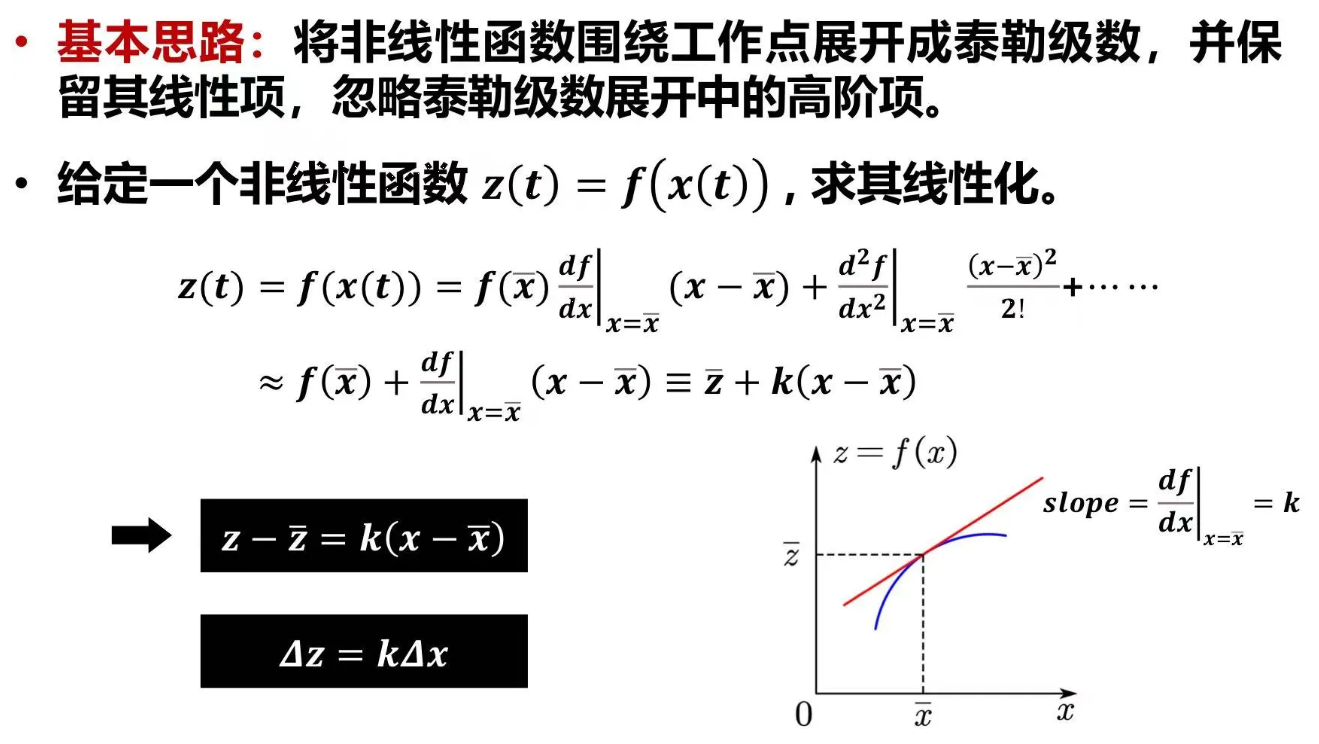
七、线性化

  • 输出和输入的关系不是线性关系时，可将非线性函数在平衡点附近线性化

    image-20241015094332695

八、时域分析

  • 总结：

    • 典型输入信号有哪些
    • 一阶系统、二阶系统在这些典型输入信号下会有怎样的输出（瞬态响应、稳态响应）
    • 高阶系统的响应受哪些因素影响：零点、极点
    • 怎样评价一个系统的性能好坏（稳准快）
      • 稳态性能指标：稳态误差
      • 瞬态性能指标：$t_r$、$t_p$ 、$M_p$ 、$t_s$、$t_d$
      • 这些性能和传递函数的零点极点有什么样的关联
    • 什么样的系统是稳定的：BIBO，极点
    • 怎样判断一个系统是否稳定：劳斯稳定判据
    • 对于一个稳定的系统，如何求其稳态误差
    • 怎样提高系统的性能：PID控制

  • 典型输入信号：

    • 阶跃信号
    • 斜坡信号
    • 抛物线函数
    • 脉冲信号
    • 正弦信号

  • 瞬态响应：初始状态到稳态的响应过程

  • 稳态响应：$t→∞$时，系统的输出

  • 瞬态性能：

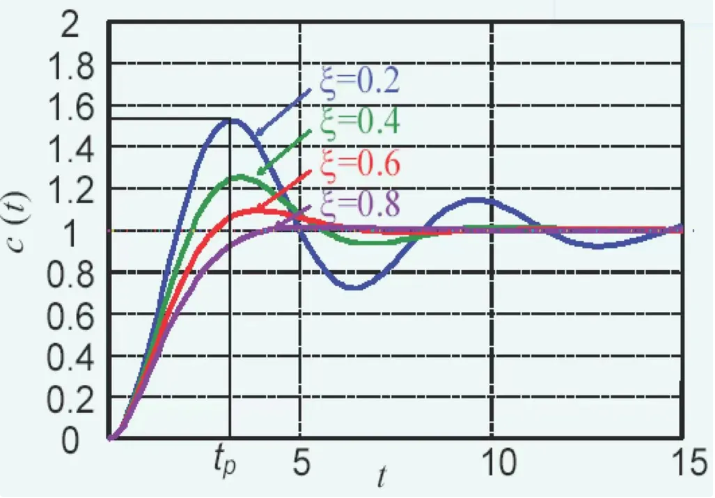
    • $t_r$ 上升时间（rise time）：有超调时为第一次到稳态所需时间；没有超调时为从稳态的10%上升到90%所需时间（快速性）
    • $t_p$ 峰值时间（peak time）：上升至第一个峰值所需时间（快速性）
    • $t_s$ 调整时间（settling time）：到达并保持在允许误差范围内所需时间（快速性）
    • $t_d$ 延时时间（delay time）：到达稳态$50\%$所需时间（快速性）
    • $M_p$ 最大超调量：$\frac{c(t_p)-c(\infty)}{c(\infty)}\times100\%$（平稳性）

  • 一阶系统：

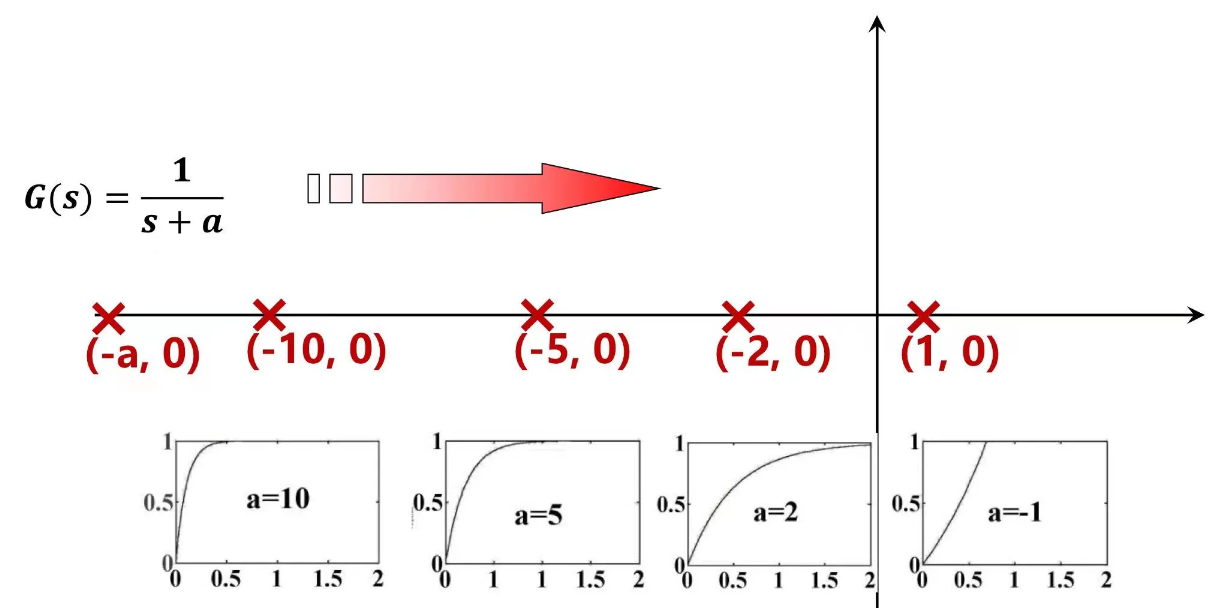
    • 传递函数 $G(s)=\frac{1}{Ts+1}$

    • 极点：$s=-\frac{1}{T}$

    • 单位阶跃响应：

      • 输出 $c(t)=1-e^{-\frac{t}{T}}$

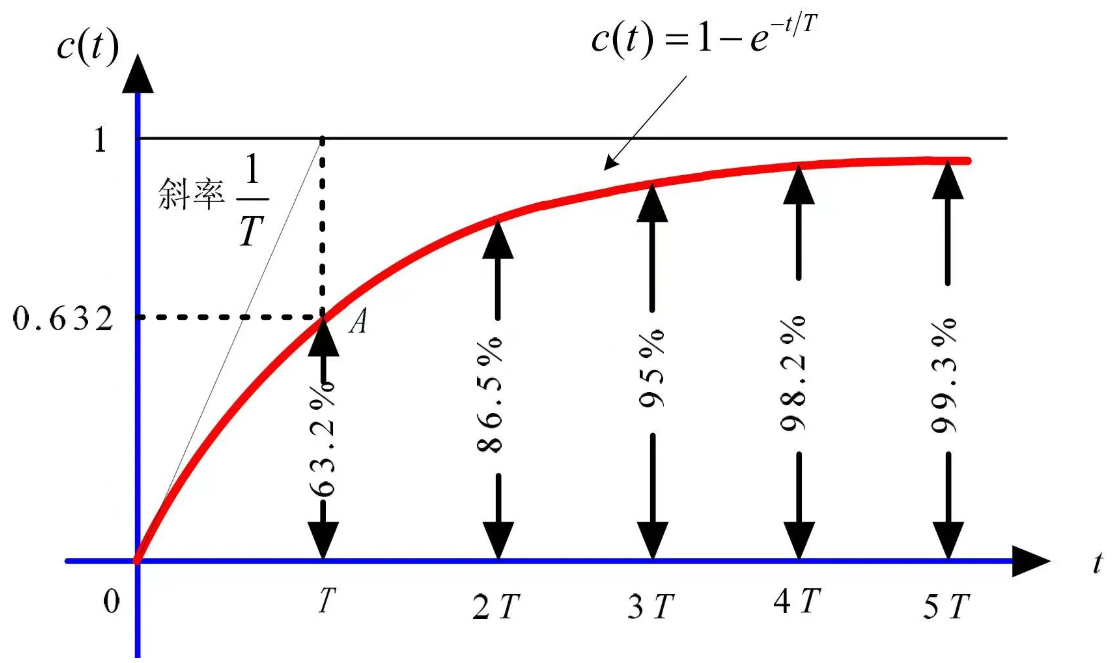
        image-20241015094421026

      • $t_s=3T$（5%误差） $t_s=4T$（2%误差）

      • T越大，极点离虚轴越近，响应越慢

        image-20241015094441680

    • 单位脉冲响应、单位斜坡响应、单位加速度响应

  • 二阶系统

    • 传递函数$G(s)=\frac{\omega_n^{2}}{s^2+2\zeta\omega_n^2S+\omega_n^2}$

    • $\zeta$：阻尼比 $\omega_n$：固有频率（无阻尼自然频率）

    • 极点：$s_1,s_2=-\zeta\omega_n\pm\omega_n\sqrt{\zeta^2-1}$

    • 过阻尼（$\zeta>1$）

      • 极点为两个不等负实根

        image-20241015094503280

      • $t_s=3\times\frac{1}{(\zeta-\sqrt{\zeta^2-1})\omega_n}$（5%误差） $t_s=4\times\frac{1}{(\zeta-\sqrt{\zeta^2-1})\omega_n}$（2%误差）

    • 临界阻尼（$\zeta=1$）

      • 极点为两个相等实根

      • 输出 $c(t)=1-e^{-\omega_nt}(1+\omega_nt)$

        image-20241015094523570

      • 斜率最大的时刻：$t=\frac{1}{\omega_n}$

      • 调整时间：到达稳态值95%，$t_s=\frac{4.7}{\omega_n}$

    • 欠阻尼（$0<\zeta<1$）

      • 一对共轭复数极点

      • $c(t)=1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}}\sin{\omega_dt}$

      • 有阻尼振荡频率 $\omega_d=\omega_n\sqrt{1-\zeta^2}$

      • 振荡周期$T_d=\frac{2\pi}{\omega_d}$

        image-20241015094541141

    • 无阻尼（$\zeta=0$）

      • 一对纯虚极点
      • $c(t)=1-\cos{\omega_nt}$

  • 高阶系统：

    • 可以只考虑主导极点的影响
    • 主导极点：距离虚轴最近的极点、附近没有零点、其他极点到虚轴的距离是这对极点到虚轴距离的五倍以上
    • 零点的影响：减小系统阻尼 $\zeta$，且越靠近虚轴，影响越明显
    • 极点的影响：增大系统阻尼，越靠近虚轴越明显
    • 若零点与极点距离很近，则他们的作用会相互抵消，对响应的影响可以忽略不计

  • 系统稳定充要条件：特征方程的所有根都在s平面左半平面（实部为负，则 e 指数为负，瞬态响应可以衰减到 0，不会发生指数爆炸）

  • 劳斯判据：

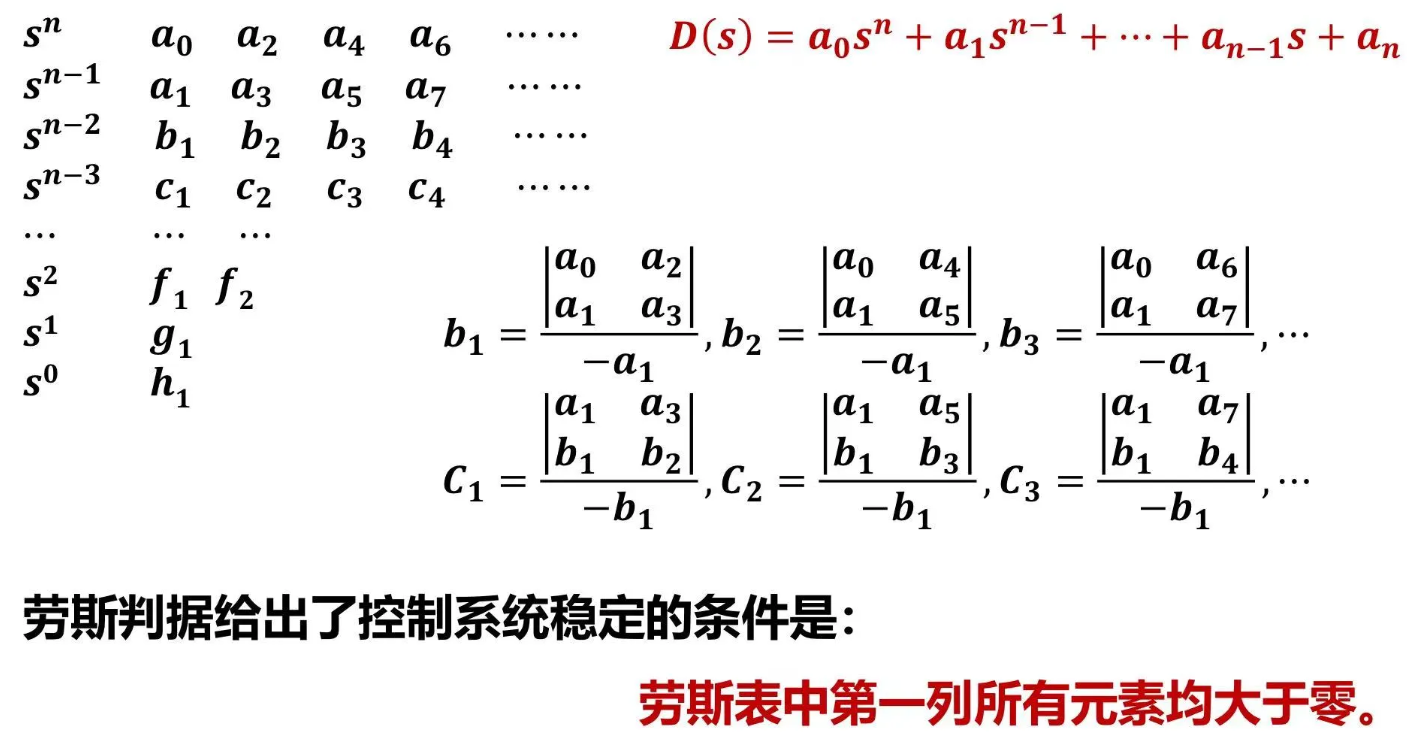
    image-20241015094604373

    • 不稳定根（右半平面根）的个数：第一列参数符号变化的次数

    • 存在一行的第一列元素为零：用 $\varepsilon$ 代替0，计算上下行符号有无变化，若不变化，则有一对虚根，若变化，则存在右半平面不稳定根

    • 存在全零行：用辅助多项式（上一行的多项式）求得根

    • 稳定裕量

      $\delta$：所有根均位于$-\delta$的左侧

      • 要判断$s$和$-\delta$的关系，所以可以令$s_1=s+\delta$，转换成判断$s_1$和 $0$ 的关系，再使用劳斯判据

  • 稳态误差：

    • 利用Laplace变换的终值定理求解

      $t→\infty$时的误差

    • 对于一个简单反馈系统

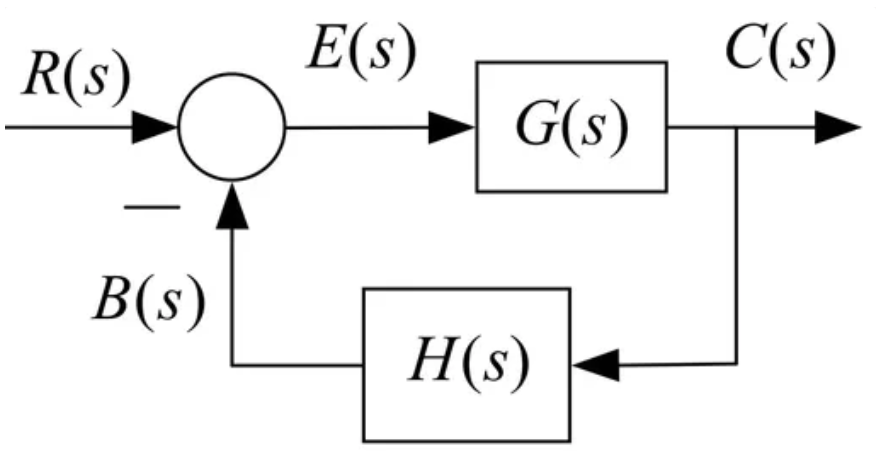
      image-20241015094720920

      与开环传递函数有关

    • 0型系统、Ⅰ型系统、Ⅱ型系统……

      image-20241015094956200

    • 稳态误差受哪些因素影响

      image-20241015095030138

    • 静态位置误差系数$K_p$：输入为单位阶跃时的稳态误差系数（上式中K的值）

    • 静态速度误差系数$K_v$：输入为单位斜坡时的稳态误差系数

    • 静态加速度误差系数$K_a$：输入为单位加速度时的稳态误差系数

    • PID控制

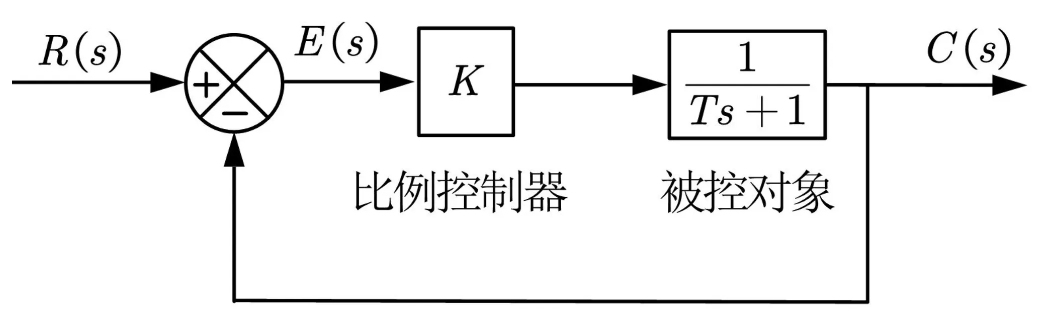
      • 比例控制（Proportional）：将误差乘以一个系数，再让系统对经比例控制后的误差进行反应

        image-20241015100357482

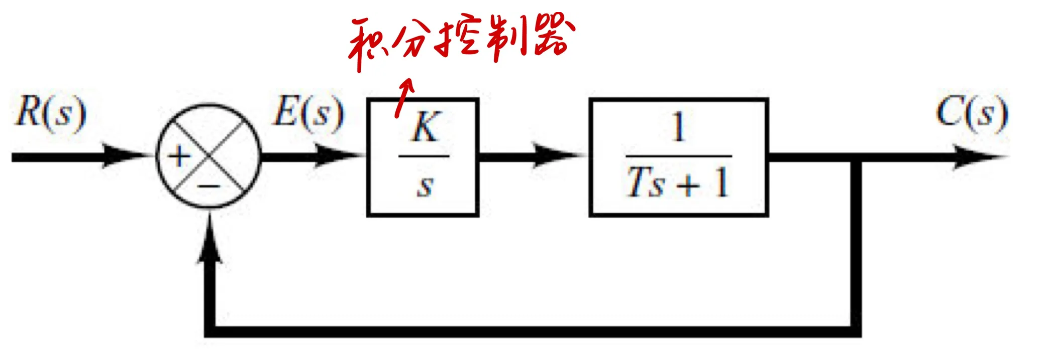
      • 积分控制（Integral）：考虑过去误差的累积量，再让系统对这个累积量进行反应

        image-20241015100422746

      • 微分控制（Differential）：考虑将来的误差，计算误差的一阶导，从而对未来的误差进行预测

        image-20241015100504687

  • $\zeta$越大，振幅衰减越快，震荡周期越长（阻力大）

    image-20241015100534995

    image-20241015100559603

九、频域分析

  • 频域分析：根据系统的开环频率特性判断闭环系统的性能
  • 频率响应：系统对正弦信号的稳态响应